题目内容
【题目】已知:![]() 关于
关于![]() 的函数
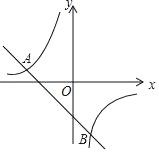
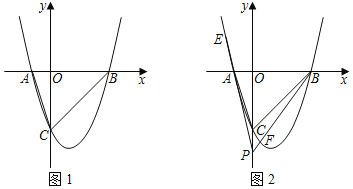
的函数![]() 的图象与坐标轴只有两个不同的交点
的图象与坐标轴只有两个不同的交点![]() 、
、![]() ,
,![]() 点坐标为
点坐标为![]() ,则
,则![]() 的面积为_____.
的面积为_____.
【答案】1或![]()
【解析】
根据k是否为0分类讨论,当k=0时,求出点B和点A的坐标,利用待定系数法求出直线AP的解析式,即可求出AP与y轴交点C的坐标,然后根据S△PAB=S△ABC+S△PBC即可求出结论;当k≠0时,根据题意可知抛物线与x轴只有一个交点,从而求出k的值,然后求出点B和点A的坐标,利用待定系数法求出直线AP的解析式,即可求出AP与y轴交点C的坐标,然后根据S△PAB=S△ABC+S△PBC即可求出结论.
解:当k=0时,![]()
设![]() 与x轴交于点A,与y轴交于点B,AP与y轴交于点C,则点A(-1,0),点B(0,1),过点P作PD⊥y轴于D,则PD=3,OA=1
与x轴交于点A,与y轴交于点B,AP与y轴交于点C,则点A(-1,0),点B(0,1),过点P作PD⊥y轴于D,则PD=3,OA=1
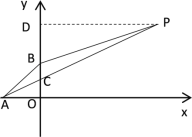
设直线AP的解析式为y=ax+b
将点A和点P的坐标代入,得
![]()
解得:![]()
∴直线AP的解析式为![]()
将x=0代入,解得y=![]()
∴点C的坐标为(0,![]() )
)
∴BC=1-![]() =
=![]()
∴S△PAB=S△ABC+S△PBC=![]() BC·OA+
BC·OA+![]() BC·PD=
BC·PD=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=1;
×3=1;
当k≠0时,![]() 是
是![]() 的二次函数,图象必与y轴交于一点B(0,1)
的二次函数,图象必与y轴交于一点B(0,1)
∵![]() 的图象与坐标轴只有两个不同的交点
的图象与坐标轴只有两个不同的交点![]() 、
、![]() ,
,
∴![]()
解得:![]()
∴二次函数解析式为![]()
将y=0代入,得![]()
解得:x1=x2=-4
∴点A的坐标为(-4,0),即AO=4
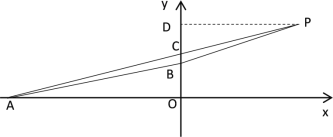
设直线AP的解析式为y=ax+b
将点A和点P的坐标代入,得
![]()
解得:![]()
∴直线AP的解析式为![]()
将x=0代入,解得y=![]()
∴点C的坐标为(0,![]() )
)
∴BC=![]() -1=
-1=![]()
∴S△PAB=S△ABC+S△PBC=![]() BC·OA+
BC·OA+![]() BC·PD=
BC·PD=![]() ×
×![]() ×4+
×4+![]() ×
×![]() ×3=
×3=![]() ;
;
综上:S△PAB=1或![]()
故答案为:1或![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目