Question

【题目】已知△ABC是⊙O的内接三角形，∠BAC的平分线交⊙O于点D．

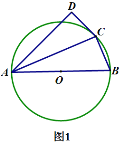
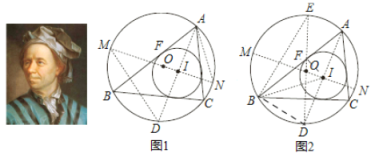
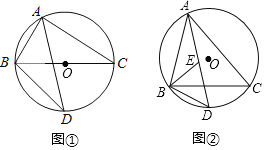
（I）如图①，若BC是⊙O的直径，BC＝4，求BD的长；

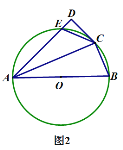
（Ⅱ）如图②，若∠ABC的平分线交AD于点E，求证：DE＝DB．

Answer 1

【答案】（I）BD＝2；（II）见解析.

【解析】

（I）连接OD，易证△DOB是等腰直角三角形，由勾股定理即可求出BD的长；

（II）由角平分线的定义结合（1）的结论即可得出∠CBD+∠CBE＝∠BAE+∠ABE，再根据三角形外角的性质即可得出∠EBD＝∠DEB，由此即可证出BD＝DE．

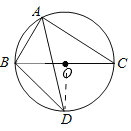
解：（I）连接OD，

∵BC是⊙O的直径，

∴∠BAC＝90°，

∵∠BAC的平分线交⊙O于点D，

∴∠BAD＝∠CAD＝45°，

∴∠BOD＝90°，

∵BC＝4，

∴BO＝OD＝2，

∴；

（II）证明：∵BE平分∠ABC，

∴∠ABE＝∠CBE．

∵∠BAD＝∠CBD，

∴∠CBD+∠CBE＝∠BAE+∠ABE．

又∵∠DEB＝BAE+∠ABE，

∴∠EBD＝∠DEB，

∴BD＝DE．