题目内容
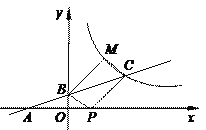
【题目】如图，射线OM上有三点A、B、C，满足OA=20cm，AB=60cm，BC=10cm，点P从点O出发，沿OM方向以1cm/秒的速度匀速运动，点Q从点C出发在线段CO上向点O匀速运动，两点同时出发，当点Q运动到点O时，点P、Q停止运动．
（1）若点Q运动速度为2cm/秒，经过多长时间P、Q两点相遇？
（2）当P在线段AB上且PA=3PB时，点Q运动到的位置恰好是线段AB的三等分点，求点Q的运动速度；
【答案】（1）经过30秒时间P、Q两点相遇；（2）点Q是速度为
cm/秒或
cm/秒．
【解析】
（1）设经过t秒时间P、Q两点相遇，列出方程即可解决问题；
（2）分两种情形求解即可.
（1）设经过t秒时间P、Q两点相遇，
则t+2t=90，
解得t=30，
所以经过30秒时间P、Q两点相遇．
（2）∵AB=60cm，PA=3PB，
∴PA=45cm，OP=65cm．
∴点P、Q的运动时间为65秒，
∵AB=60cm，
AB=20cm，
∴QB=20cm或40cm，
∴点Q是速度为
=cm/秒或
=cm/秒．
练习册系列答案
相关题目
