题目内容
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(Ⅰ)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=32°,求∠P的大小;
(Ⅱ)如图②,D为优弧ADC上一点,且DO的延长线经过AC的中点E,连接DC与AB相交于点P,若∠CAB=16°,求∠DPA的大小.
【答案】解:(Ⅰ)连接OC,如图①,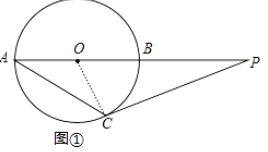
∵PC为切线,
∴OC⊥PC,
∴∠OCP=90°,
∵OA=OC,
∴∠OCA=∠CAB=32°,
∴∠POC=∠OCA+∠CAB=64°,
∴∠P=90°﹣∠POC=90°﹣64°=26°;
(Ⅱ)如图②,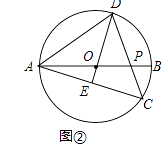
∵点E为AC的中点,
∴OD⊥AC,
∴∠OEA=90°,
∴∠AOD=∠CAB+∠OEA=16°+90°=106°,
∴∠C= ![]() ∠AOD=53°,
∠AOD=53°,
∴∠DPA=∠BAC+∠C=16°+53°=69°
【解析】(Ⅰ)连接OC,如图①,根据切线的性质得∠OCP=90°,再根据等腰三角形的性质得到∠OCA=∠CAB=32°,则利用三角形外角性质可计算出∠POC,然后利用互余计算∠P的度数;(Ⅱ)如图②,根据垂径定理的推论,由点E为AC的中点得到OD⊥AC,则利用三角形外角性质得∠AOD=∠CAB+∠OEA=106°,再根据圆周角定理得到∠C=![]() ∠AOD=53°,然后利用三角形外角性质可计算出∠DPA的度数.
∠AOD=53°,然后利用三角形外角性质可计算出∠DPA的度数.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班
分别选5名同学参加“国防知识”比赛,
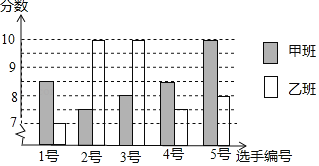
其预赛成绩如图所示:
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
甲班 | 8.5 | 8.5 |
|
乙班 | 8.5 |
| 10 |
(2)分别求甲乙两班的方差,并从稳定性上分析哪个班的成绩较好.
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
消费卡 | 消费方式 |
普通卡 | 35元/次 |
白金卡 | 280元/张,凭卡免费消费10次再送2次 |
钻石卡 | 560元/张,凭卡每次消费不再收费 |
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式.