��Ŀ����
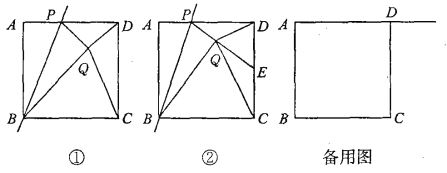
����Ŀ����ͼ������֪������ABCD�ı߳�Ϊ1����P��AD���ϵ�һ�����㣬��A����ֱ��BP�ĶԳƵ��ǵ�Q������PQ��DQ��CQ��BQ����AP��x��
��1��BQ��DQ����Сֵ��_______����ʱx��ֵ��_______��
��2����ͼ������PQ���ӳ��߽�CD���ڵ�E��������CQD��90����
����֤����E��CD���е㣻 ����x��ֵ��
��3������P������AD�ϵ�һ�����㣬��ֱ��д������CDQΪ����������ʱx��ֵ��
���𰸡���1��![]() ��
��![]() ;(2) �����������������
;(2) �����������������![]() ;(3) 2��
;(3) 2��![]() ��
��![]() ��2+
��2+![]() ��
��
��������
���������(1)��������֮��,�߶���̿�֪,��Q���߶�BD��ʱBQ��DQ��ֵ��С,��BD�ij���,���ù��ɶ����������;�ٸ�����PDQ�ǵ���ֱ�����������x��ֵ;
(2) ���ɶԳƿ�֪AB=BQ=BC,�����BCQ=��BQC.������BQE=��BCE=90��,��֪��EQC=��ECQ,�Ӷ�EQ=EC.�ٸ�����CQD=90���ɵ���DQE+��CQE=90��, ��QCE+��QDE=90��,����EQC=��ECQ, ������QDE=��DQE���Ӷ�EQ=ED.�õ�E��CD���е㣻����Rt��PDE�У�PE= PQ+QE=x+![]() ��PD=1��x��PQ=x�����ݹ��ɶ����������x��ֵ.
��PD=1��x��PQ=x�����ݹ��ɶ����������x��ֵ.
(3) ��CDQΪ���������η��������:��CDΪ��,�Ե�C ΪԲ��,��CD�ij�Ϊ�뾶����,�������㼴Ϊʹ����CDQΪ���������ε�Q��; ��CDΪ�ױ�ʱ,��CD�Ĵ�ֱƽ����,��![]() �Ľ��㼴Ϊ��CDQΪ���������ε�Q��,���� 3��Q��,��ôҲ����3��P��,��������,����ֱ�������ε�������֮����.
�Ľ��㼴Ϊ��CDQΪ���������ε�Q��,���� 3��Q��,��ôҲ����3��P��,��������,����ֱ�������ε�������֮����.
�����������1��![]() ��
��![]() ��
��
��2����֤������������ABCD�У�
AB=BC����A=��BCD=90�㣮
��Q��ΪA�����BP�ĶԳƵ㣬
��AB=QB����A=��PQB=90�㣬
��QB=BC����BQE=��BCE��
���BQC=��BCQ��
���EQC=��EQB����CQB=��ECB����QCB=��ECQ��
��EQ=EC��
��Rt��QDC��
�ߡ�QDE=90�㩁��QCE��
��DQE=90�㩁��EQC��
���QDE=��DQE��
��EQ=ED��
��CE=EQ=ED����EΪCD���е㣮
�ڡ�AP=x��AD=1��
��PD=1��x��PQ=x��CD=1��
��Rt��DQC��
��EΪCD���е㣬
��DE=QE=CE=![]() ��
��
��PE=PQ+QE=x+![]() ��
��
��![]() ��
��
��� x=![]() ��
��
��3����CDQΪ����������ʱx��ֵΪ2-![]() ��
��![]() ��2+
��2+![]() ��
��
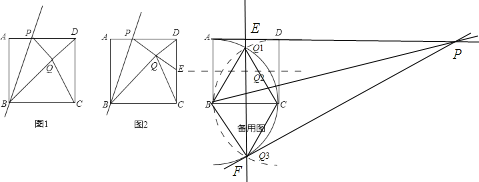
��ͼ���Ե�BΪԲ�ģ���AB�ij�Ϊ�뾶�������Ե�CΪԲ�ģ���CD�ij�Ϊ�뾶�����������ֱ���Q1��Q3����ʱ��CDQ1����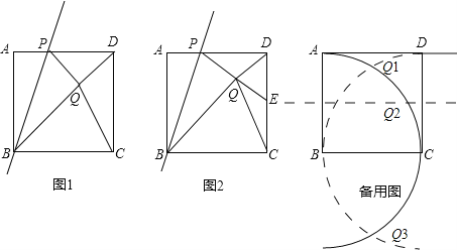
��CDQ2��CDΪ�ĵ������Σ�
���¶Դ�Q1��Q2��Q3���ֱ����۸��Ե�P�㣬����AP��ֵ��
����Q:��ͼ�������ߣ�����BQ1��CQ1����PQ1��BQ1��AD��P������Q1����EF��AD��E����BC��F��
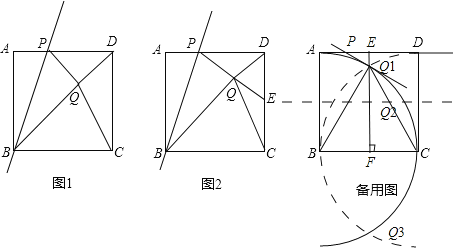
�ߡ�BCQ1Ϊ�ȱ������Σ�������ABCD�߳�Ϊ1��
��![]() ��
��![]() ��
��
���ı���ABPQ1�У�
�ߡ�ABQ1=30����
���APQ1=150����
���PEQ1Ϊ��30����ֱ�������Σ�
��PE=![]() ��
��
��AE=![]() ��
��
��x=AP=AE-PE=2-![]() ��
��
������Q2����ͼ�������ߣ�����BQ2��AQ2������Q2��PG��BQ2����AD��P������BP������Q2��EF��CD��E����AB��F��

��EF��ֱƽ��CD��
��EF��ֱƽ��AB��
��AQ2=BQ2��
��AB=BQ2��
���ABQ2Ϊ�ȱ������Σ�
���ı���ABQP�У�
�ߡ�BAD=��BQP=90��, ��ABQ=60��,
���APE=120��
���EQ2G=��DPG=180��-120��=60����
��![]() ��
��
��EG=![]() ��
��
��DG=DE+GE=![]() -1��
-1��
��PD=1-![]() ��
��
��x=AP=1-PD=![]() ��
��
����Q3����ͼ�������ߣ�����BQ1��CQ1��BQ3��CQ3������Q3��BQ3��PQ3����AD���ӳ�����P������BP������Q1����EF��AD��E����ʱQ3��EF�ϣ�������Q3��F�غϣ�
�ߡ�BCQ1Ϊ�ȱ������Σ���BCQ3Ϊ�ȱ������Σ�BC=1��
��![]() ��
��![]() ��
��
��![]() ��
��
���ı���ABQ3P��
�ߡ�ABF=��ABC+��CBQ3=150����
���EPF=30����
��EP=![]() ,EF=
,EF=![]() ��
��
��AE=![]() ��
��
��x=AP=AE+PE=![]() +2��
+2��
������������CDQΪ����������ʱx��ֵΪ2��![]() ��
��![]() ��2+
��2+![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ������������ʣ���Щ��ѡ��רҵ�Ľ������Ķ������壬ij�������ĵ����ѷ�ʽ���£�
���ѿ� | ���ѷ�ʽ |
��ͨ�� | 35Ԫ/�� |
�� | 280Ԫ/�ţ�ƾ���������10������2�� |
��ʯ�� | 560Ԫ/�ţ�ƾ��ÿ�����Ѳ����շ� |
�������ѿ�ʹ������Ϊһ�꣬ÿλ�˿�ֻ�ܹ���һ�ſ�����ֻ�ޱ���ʹ��
������ÿ��ȥ�ý�������6�Σ�Ӧѡ���������ѷ�ʽ�����㣿
������һ����ȥ�ý������Ľ���x�Σ�xΪ���������������ܷ���ΪyԪ����ֱ�д��ѡ����ͨ���ѺͰ����ѵ�y��x�ĺ�����ϵʽ��
������ijλ�˿�ÿ��ȥ�ý������Ľ�������18�Σ���ͨ�����������λ�˿�ѡ�����������ѷ�ʽ��