题目内容
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),
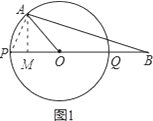
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求![]() 的值(图3).
的值(图3).

【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】(1)根据直角三角形的性质求出∠B的度数,得到∠AOB的度数,再根据弧长的计算公式进行求解即可;
(2)连接AP,过点A作AM⊥BP于M,根据特殊角的三角函数值和已知条件求出AM,再根据BM=OM+OB,求出BM,最后根据勾股定理求出AB;
(3)连接MQ,根据PQ是圆O的直径和AO⊥PM,得出ON∥MQ,求出ON=![]() AO,设ON=x,则AO=4x,根据OA的值求出x的值,再根据PN=
AO,设ON=x,则AO=4x,根据OA的值求出x的值,再根据PN=![]() ,求出PN,最后根据特殊角的三角函数值即可得出答案.
,求出PN,最后根据特殊角的三角函数值即可得出答案.
解:(1)∵直线AB与圆O相切,
∴∠OAB=90°,
∵OQ=QB=1,
∴OA=1,OB=2,
∴OA=![]() OB,
OB,
∴∠B=30°,
∴∠AOB=60°,
∴AQ=![]() =
=![]() ;
;
(2)如图1,
连接AP,过点A作AM⊥BP于M,
∵∠AOB=120°,∴∠AOP=60°,
∵OM=![]() ,∴BM=OM+OB=
,∴BM=OM+OB=![]() +2=
+2=![]() ,
,
∴AB=![]() =
=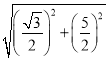 =
=![]() ;
;
(3)如图2,连接MQ,
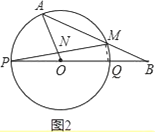
∵PQ为圆O的直径,∴∠PMQ=90°,
∵ON⊥PM,∴AO∥MQ,
∵PO=OQ,
∴ON=![]() MQ,
MQ,
∵OQ=BQ,
∴MQ=![]() AO,
AO,
∴ON=![]() AO,
AO,
设ON=x,则AO=4x,
∵OA=1,
∴4x=1,
∴x=![]() ,
,
∴ON=![]() ,
,
∴PN=![]() =
=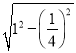 =
=![]() ,
,
![]() =
=![]() =
=![]() .
.

【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下: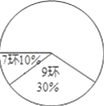
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.

