��Ŀ����
��֪A��A��������y=
x2�����㣬A1B1��A3B3�ֱ�ֱ��x�ᣬ����ֱ�ΪB1��B3����C���߶�A1A3���е㣬����C��CB2��ֱ��x�ᣬ����ΪB2��CB2���������ڵ�A2��
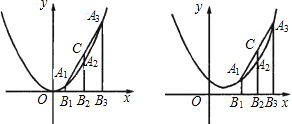
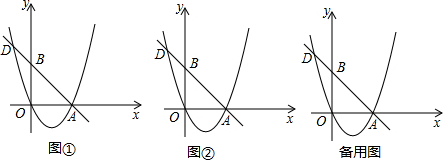
��1����ͼ1����֪A1��A3����ĺ���������Ϊ1��3�����߶�CA2�ij���
��2����ͼ2������������y=
x2��������y=
x2-x+1����A1��A2��A3����ĺ�����Ϊ�����������������������䣬���߶�CA2�ij���
��3������������y=
x2��Ϊ������y=ax2+bx+c��a��0����A1��A2��A3����ĺ�����Ϊ���������������������䣬�Բ����߶�CA2�ij�����a��b��c��ʾ����ֱ��д���𰸣���
| 1 |
| 2 |

��1����ͼ1����֪A1��A3����ĺ���������Ϊ1��3�����߶�CA2�ij���
��2����ͼ2������������y=
| 1 |
| 2 |
| 1 |
| 2 |
��3������������y=
| 1 |
| 2 |
��1����A1��A3�ĺ���������Ϊ1��3��
��A1B1=
��12=
��A3B3=
��32=
��
����֪�ɵ�A1B1��CB2��A3B3��
�֡�CΪA1A3���е㣬
��B2ΪB1B3���е㣬
��B2��ĺ�����Ϊ2��
��A2B2=
��22=2��
��CB2=
��A1B1+A3B3��
=
��
+
��+
��CA2=CB2-A2B2=
-2
=
��
��2����A1��A2��A3����ĺ���������Ϊn-1��n��n+1��
��A1B1=
��n-1��2-��n-1��+1��A2B2=
n2-n+1��
A3B3=
��n+1��2-��n+1��+1��
����֪�ɵ�A1B1��A3B3��AB2��
��CB2=
��A1B1+A3B3��
=
[
��n-1��2-��n-1��+1+
��n+1��2-��n+1��+1]
=
n2-n+
��
��CA2=CB2-A2B2=
n2-n+
-��
n2-n+1��=
��
��3����a��0ʱ��CA2=a��
��A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
����֪�ɵ�A1B1��CB2��A3B3��
�֡�CΪA1A3���е㣬
��B2ΪB1B3���е㣬
��B2��ĺ�����Ϊ2��
��A2B2=
| 1 |
| 2 |
��CB2=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 5 |
| 2 |
��CA2=CB2-A2B2=
| 5 |
| 2 |
=
| 1 |
| 2 |
��2����A1��A2��A3����ĺ���������Ϊn-1��n��n+1��
��A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
A3B3=
| 1 |
| 2 |
����֪�ɵ�A1B1��A3B3��AB2��
��CB2=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
��CA2=CB2-A2B2=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��3����a��0ʱ��CA2=a��

��ϰ��ϵ�д�
�����Ŀ
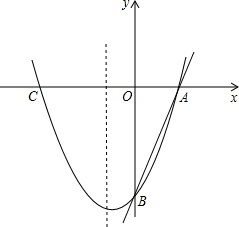
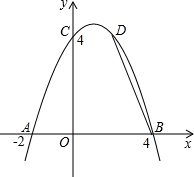
 A��m��0����B��0��n����
A��m��0����B��0��n����