题目内容
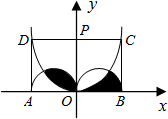
如图:矩形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线y=-
x2+
x上,矩形的顶点均为动点,且矩形在抛物线与x轴围成的区域里.
(1)设点A的坐标为(x,y),试求矩形的周长p关于变量x的函数的解析式,并写出x的取值范围;
(2)是否存在这样的矩形ABCD,它的周长p=9?试证明你的结论.

| 2 |
| 3 |
| 8 |
| 3 |
(1)设点A的坐标为(x,y),试求矩形的周长p关于变量x的函数的解析式,并写出x的取值范围;
(2)是否存在这样的矩形ABCD,它的周长p=9?试证明你的结论.

(1)令-
x2+
x=0,
得:x1=0,x2=4,
则抛物线与坐标轴两交点的坐标为O(0,0)和E(4,0),
设OB=x(0<x<2),由抛物线的对称性可知EC=x,则BC=4-2x,
P=2(4-2x+y)=2(4-2x-
x2+
x)=-
x2+
x+8(0<x<2).
(2)不存在.
先假设存在周长为9的矩形ABCD,则-
x2+
x+8=9,
化简得:4x2-4x+3=0,
则有△=16-48<0,
∴方程无实数根,即不存在这样的矩形.
| 2 |
| 3 |
| 8 |
| 3 |
得:x1=0,x2=4,
则抛物线与坐标轴两交点的坐标为O(0,0)和E(4,0),
设OB=x(0<x<2),由抛物线的对称性可知EC=x,则BC=4-2x,
P=2(4-2x+y)=2(4-2x-
| 2 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(2)不存在.
先假设存在周长为9的矩形ABCD,则-
| 4 |
| 3 |
| 4 |
| 3 |
化简得:4x2-4x+3=0,
则有△=16-48<0,
∴方程无实数根,即不存在这样的矩形.

练习册系列答案
相关题目


 若不是,请说明理由;
若不是,请说明理由;