题目内容
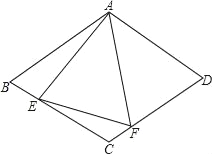
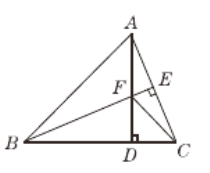
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证△ACD≌△BFD
(2)求证:BF=2AE;
(3)若CD=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)见解析;(3)AD =2+![]()
【解析】
(1)先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等;
(2)根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证;
(3)根据全等三角形对应边相等可得DF=CD,然后利用勾股定理列式求出CF,再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF,然后根据AD=AF+DF代入数据即可得解.
(1)∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
∠CAD=∠CBE,AD=BD,∠ADC=∠BDF=90°,
∴△ACD≌△BFD(ASA)
(2)由(1)可知:BF=AC
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(3) ∵△ACD≌△BFD,
∴DF=CD=![]() ,
,
在Rt△CDF中,CF=![]() ,
,
∵BE⊥AC,AE=EC,
∴AF=CF=2.
∴AD=AF+DF=2+![]()

 名校课堂系列答案
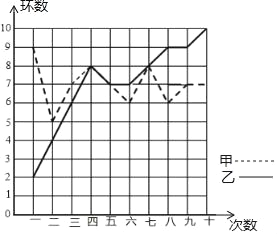
名校课堂系列答案【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.