题目内容
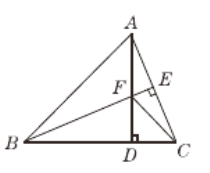
【题目】如图，在△ABC中，D为AB边上一点，E为CD中点，AC=
，∠ABC=30°，∠A=∠BED=45°，则BD的长为（ ）
A. 
B. 
+1﹣
C. ﹣ D. ﹣1
【答案】D
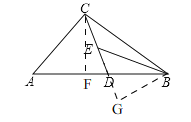
【解析】解：如图，过C作CF⊥AB于F，过点B作BG⊥CD于G．在Rt△BEG中，∠BED=45°，则GE=GB．在Rt△AFC中，∠A=45°，AC=
，则AF=CF=
=1．在Rt△BFC中，∠ABC=30°，CF=1，则BC=2CF=2，BF=
CF=，设DF=x，CE=DE=y，则BD=﹣x，∴△CDF∽△BDG，∴
=
=
，∴
=
=
，∴DG=
，BG=
．∵GE=GB，∴y+=，∴2y2+x（﹣x）=﹣x．在Rt△CDF中，∵CF2+DF2=CD2，∴1+x2=4y2，∴
+x（﹣x）=﹣x，整理得：x2﹣（2+2）x+2﹣1=0，解得：x=1+﹣
或1+﹣（舍弃），∴BD=﹣x=﹣1．故选D．
夺冠金卷全能练考系列答案
【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=
x+5，（x单位：年，1≤x≤6且x为整数）；后4年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=-
x+
（x单位：年，7≤x≤10且x为整数）．假设每年的公租房全部出租完．另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金z（单位：元/m2）与时间x（单位：年，1≤x≤10且x为整数）满足一次函数关系如下表：
z（元/m2） | 50 | 52 | 54 | 56 | 58 | … |
x（年） | 1 | 2 | 3 | 4 | 5 | … |
（1）求出z与x的函数关系式；
（2）求政府在第几年投入的公租房收取的租金最多，最多为多少百万元；
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高a%，这样可解决住房的人数将比第6年减少1.35a%，求a的值．
（参考数据：
，
，
）
【题目】下表给出了某班6名同学的身高情况(单位：cm).
学生 | A | B | C | D | E | F | |
身高(单位：cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | －1 | ＋2 | ____ | －3 | ＋4 | ____ |
(1)完成表中空的部分；
(2)他们6人中最高身高比最矮身高高多少？
(3)如果身高达到或超过平均身高时叫达标身高，那么这6名同学身高的达标率是多少？
