题目内容
【题目】小明将一根长为20厘米的铁丝剪成两段，然后分别围成两个正方形。设其中一段铁丝长为x厘米。
（1）设较长的一段铁丝长为xcm，请计算出这两个正方形的面积之差；
（2）是否存在合适的x的值，使两个正方形的面积刚好相差5cm2？请说明理由.
【答案】（1）
x-25；（2）即当x=12时，这两个正方形的面积刚好相差5cm2．
【解析】
（1）根据正方形的周长公式得到其边长，然后计算其面积即可；
（2）假设存在这样的x值，根据面积相差5cm2，列出关于x的方程，然后解方程．
（1）依题意得，
x-25．
即这两个正方形的面积之差为：x-25．
（2）假设存在这样的x值，使两个正方形的面积刚好相差5cm2．则x-25=5，
解得x=12．符合题意．
即当x=12时，这两个正方形的面积刚好相差5cm2．
练习册系列答案
相关题目
【题目】为了解上一次八年级数学测验成绩情况，随机抽取了40名学生的成绩进行统计分析，这40名学生的成绩数据如下：
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
（1）将样本数据适当分组，制作频数分布表：
分 组 |
|
|
|
|
|
频 数 |
|
|
|
|
|
（2）根据频数分布表，绘制频数直方图：
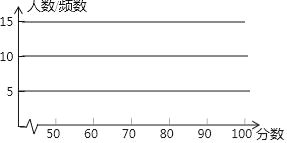
（3）从图可以看出，这40名学生的成绩都分布在什么范围内？分数在哪个范围的人数最多？