��Ŀ����
����Ŀ��ij������Ӽס���������Ա����ͬ�������¸����10�Σ�ÿ����ҵijɼ������ͼ��ʾ��
��1���뽫�±��������������ο���ʽ������S2=![]() [��x1��
[��x1��![]() ��2+��x2��
��2+��x2��![]() ��2+��+��xn��
��2+��+��xn��![]() ��2]��
��2]��
ƽ���� | ���� | ��λ�� | |
�� | 7 | �� �� | 7 |
�� | �� �� | 5.4 | �� �� |
��2���������������ͬ�ĽǶȶ���β��Խ������
�ٴ�ƽ�����ͷ������Ͽ����� ���ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ����� ���ijɼ���Щ��
����������ѡ����óɼ���9�����ң���Ҫѡһ�˲���������Ϊѡ˭�μӣ���˵�����ɣ�
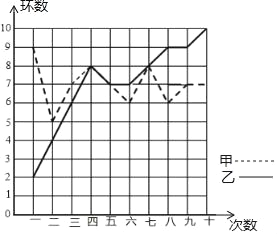
���𰸡���1��1.2��7��7.5����2���ף��ң��ң����ɼ�����.
������������: ��1������ͳ�Ʊ������ƽ�����������λ���Ķ��壬���������Ҫ��д�����ݣ�
��2�����ɷֱ��ƽ�����ͷ������������ֽ��бȽϣ�
���ɷֱ��ƽ��������λ�����������ֽ��бȽϣ�
���ɴӾ���������ֵ����˵�����ɣ�
���:
�⣺��1���ķ���![]() [��9��7��2+��5��7��2+4����7��7��2+2����8��7��2+2����6��7��2]=1.2��
[��9��7��2+��5��7��2+4����7��7��2+2����8��7��2+2����6��7��2]=1.2��
�ҵ�ƽ��������2+4+6+8+7+7+8+9+9+10����10=7��
�ҵ���λ������7+8����2=7.5��
������£�
ƽ���� | ���� | ��λ�� | |
�� | 7 | 1.2 | 7 |
�� | 7 | 5.4 | 7.5 |
��2���ٴ�ƽ�����ͷ������Ͽ����ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ����ҵijɼ���Щ��
��ѡ�Ҳμ���
���ɣ��ۺϿ������Ӹ��ȶ�����������Ȳ�ҷ�����Ȼ���ȶ��������и߰л��������࣬�ɼ������������DZ��������������ֵ��Ӧѡ�ң�
�ʴ�Ϊ����1��1.2��7��7.5����2���ټף����ң�

 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д�����Ŀ��Ϊ�˽���һ�ΰ��꼶��ѧ����ɼ�����������ȡ��40��ѧ���ijɼ�����ͳ�Ʒ�������40��ѧ���ijɼ��������£�
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
��1�������������ʵ����飬����Ƶ���ֲ�����
�� �� | �� �� | �� �� | �� �� | �� �� | �� �� |
Ƶ �� | �� �� | �� �� | �� �� | �� �� | �� �� |
��2������Ƶ���ֲ���������Ƶ��ֱ��ͼ��
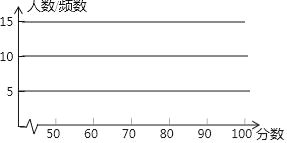
��3����ͼ���Կ�������40��ѧ���ijɼ����ֲ���ʲô��Χ�ڣ��������ĸ���Χ��������ࣿ