题目内容
【题目】如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．
【答案】6.
【解析】试题分析：
由已知条件易证Rt△AEF≌Rt△DCE，从而可得AE=CD，AF=DE，结合矩形ABCD的周长为32，DE=4可得AE+4+DC=16，即AE+4+AE=16，由此可解得AE=6.
试题解析：
在Rt△AEF和Rt△DEC中，EF⊥CE．
∴∠FEC=90°．
∴∠AEF+∠DEC=90°．
而∠ECD+∠DEC=90°．
∴∠AEF=∠ECD．
在Rt△AEF与Rt△DCE中，
∵
，
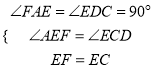∴Rt△AEF≌Rt△DCE（AAS）．
∴AE=CD．
AD=AE+4．
∵矩形ABCD的周长为32cm．
∴2（AE+ED+DC）=32，即2（2AE+4）=32，
整理得：2AE+4=16
解得：AE=6（cm）．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
