题目内容
【题目】已知凸四边形ABCD中,∠A=∠C=90°.
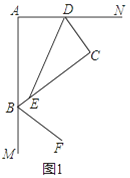
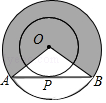
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
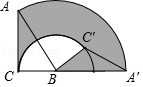
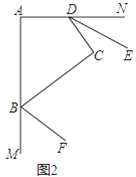
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
【答案】见解析
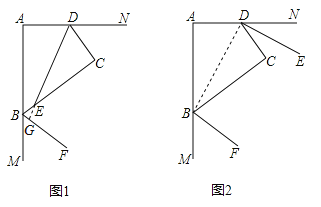
【解析】试题分析:(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
试题解析:解:(1)DE⊥BF.证明如下:
延长DE交BF于点G.∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,∴∠ABC+∠ADC=180°.∵∠ABC+∠MBC=180°,∴∠ADC=∠MBC.∵DE、BF分别平分∠ADC、∠MBC,∴∠EDC=![]() ∠ADC,∠EBG=
∠ADC,∠EBG=![]() ∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
(2)DE∥BF.证明如下:
连接BD.∵DE、BF分别平分∠NDC、∠MBC,∴∠EDC=![]() ∠NDC,∠FBC=
∠NDC,∠FBC=![]() ∠MBC.
∠MBC.
∵∠ADC+∠NDC=180°,∠ADC=∠MBC,∴∠MBC+∠NDC=180°,∴∠EDC+∠FBC=90°.
∵∠C=90°,∴∠CDB+∠CBD=90°,∴∠EDC+∠CDB+∠FBC+∠CBD=180°,即∠EDB+∠FBD=180°,∴DE∥BF.

【题目】把正方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
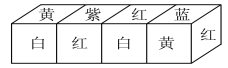
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |