题目内容
【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长. 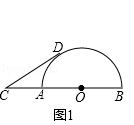
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积. 
【答案】
(1)2;6;6
(2)解:连接OD,
∵线段CD所在直线与半圆O相切,
∴OD⊥CD,
∵OC=4,OD=2,
∴∠C=30°,
∴∠COD=60°,
∴∠BOD=120°,
∴弧BD的长为: ![]() =
= ![]() π
π
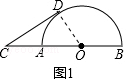
(3)解:∵CM=DM,
∴CD=2CM,
由切割线定理得,CMCD=CACB=12,
解得,CM= ![]() ,
,
则CD=2 ![]() ,
,
∴等边△CDE面积为: ![]() ×2
×2 ![]() ×2
×2 ![]() ×sin60°=6
×sin60°=6 ![]()
【解析】解:(1)发现:当点D与点A重合时,CD最小,CD的最小值是2, 当点D与点B重合时,CD最大,CD的最大值是6,
当OD⊥CB时,CD最小,△CBD的面积最大,最大值为: ![]() ×6×2=6,
×6×2=6,
故答案为:2;6;6;
发现:根据圆的性质、三角形的面积公式计算;
思考:连接OD,根据切线的性质得到OD⊥CD,根据直角三角形的性质求出∠C,得到∠BOD,根据弧长公式计算即可;
探究:根据切割线定理求出CD,根据等边三角形的面积公式计算即可.

练习册系列答案
相关题目