题目内容
【题目】我们定义：从三角形一个顶点引出一条射线与对边相交，如果顶点与交点之间的线段把这个三角形分割成两个小的等腰三角形，那么我们就说原三角形为“可分割三角形”，这条线段叫做这个三角形的分割线.
（1）已知
，
，
，则可分割三角形.（填“是”或“不是”）
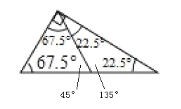
（2）小愿研究发现，下图的两个三角形都是可分割三角形，请你画出每个三角形的分割线，并标出分成的等腰三角形顶角的度数.
（3）若是可分割三角形，
，
为钝角，请通过画图的方式写出所有可能的度数（画出图形，标示的度数）.
【答案】（1）是；（2）见解析；（3）见解析，
的度数为
或
或
.
【解析】
（1）根据等腰三角形的性质作图求出各角度即可证明；
（2）根据可分割三角形的定义即可作图求解；
（3）根据题意分情况讨论作图即可求解.
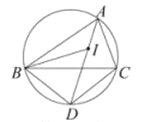
解：（1）∵在
中
，
，
∴∠ABC=∠C=72°，
如图，作BD=BC，
∴∠BDC=72°，∠DBC=36°，
∴∠ABD=∠ABC-∠DBC=36°，
∴△ABD与△BDC都是等腰三角形，
则是可分割三角形.
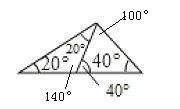
（2）如图，过直角顶点作一条直线，将直角三角形分成两个小等腰三角形，它们的顶角分别为45°和135°；过钝角顶点作一条直线，将钝角三角形分成两个小等腰三角形，它们的顶角分别为100°和140°；
（3）如图中，当
是特异线时，如果
，
则
，
如果
，
，
则
，
如果
，
，
则
（不合题意舍去），
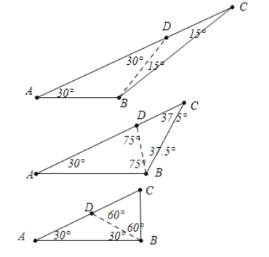
如图中，当
是特异线时，
，
，则
，
符合条件的的度数为或或.
如果
，，
则
如果，，
则
（不合题意舍弃）
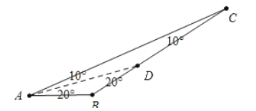
如图中，当是特异线时，，，
则
当
为特异线时，不合题意.
符合条件的的度数为或或
口算心算速算应用题系列答案
同步拓展阅读系列答案
【题目】某直销公司现有
名推销员，
月份每个人完成销售额（单位：万元），数据如下：
整理上面的数据得到如下统计表：
销售额 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
（1）统计表中的
；
；
（2）销售额的平均数是 ；众数是 ；中位数是 .
（3）
月起，公司为了提高推销员的积极性，将采取绩效工资制度：规定一个基本销售额，在基本销售额内，按
抽成；从公司低成本与员工愿意接受两个层面考虑，你认为基本销售额定位多少万元？请说明理由.
