题目内容
【题目】如图，⊙O的半径为5cm，弦AB为8cm，P为弦AB上的一动点，若OP的长度为整数，则满足条件的点P有____个．
【答案】5
【解析】
首先过点O作OC⊥AB于点C,连接OA,由垂径定理可求得OP的取值范围为3
,而OP=3的点只有一个,OP=4的点有2个,OP=5的点有2个,故符合条件的点P有5个.
过O作OC⊥AB于C，连接OA；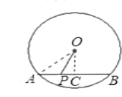
Rt△OAC中，OA=5cm，AC=4cm；
∴OC2=OA2AC2；
∴OC=3；
故OP=3cm，或4cm，或5cm；
当OP=3cm时，P与C点重合，有一个符合条件的P点；
当OP=4cm时，P位于AC或BC之间，有两个符合条件的P点；
当OP=5cm时，P与A或B重合，有两个符合条件的P点；
故满足条件的P点有5个.
练习册系列答案
相关题目
