题目内容
【题目】八年级的小明同学通到这样一道数学题目：△ABC为边长为4的等边三角形，E是边AB边上任意一动点，点D在CB的延长线上，且满足AE＝BD．
（1）如图①，当点E为AB的中点时，DE＝ ；
（2）如图②，点E在运动过程中，DE与EC满足什么数量关系？请说明理由；
（3）如图③，F是AC的中点，连接EF．在AB边上是否存在点E，使得DE+EF值最小？若存在，求出这个最小值；若不存在，请说明理由．（直角三角形中，30°所对的边是斜边的一半）
【答案】（1）2
；（2）DE＝CE，理由见解析；（3）这个最小值为2
；
【解析】
（1）如图①，过点E作EH⊥BC于H，由等边三角形的性质可得BE=DB=AE=2，由直角三角形的性质可求BH=1，EH
，由勾股定理可求解；
（2）如图②，过E作EF∥BC交AC于F，可证△AEF是等边三角形，AE=EF=AF=BD，由“SAS”可证△DBE≌△EFC，可得DE=CE；
（3）如图③，将△ABC沿AB翻折得到△ABC'，连接C'F交AB于点E'，连接CE'，DE'，过点F作FH⊥AC'于点H，由“SAS”可证△ACE'≌△AC'E'，可得C'E'=CE'，可得当点C'，点E'，点F三点共线时，DE+EF的值最小，由勾股定理可求最小值.
（1）如图①，过点E作EH⊥BC于H，
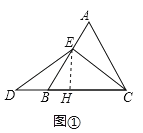
∵△ABC为边长为4的等边三角形，点E是AB的中点，
∴AE=BE=2=DB，∠ABC=60°，且EH⊥BC，
∴∠BEH=30°，
∴BH=1，EHBH，
∴DH=DB+BH=2+1=3，
∴DE
.
故答案为：；
（2）DE=CE.理由如下：
如图②，过E作EF∥BC交AC于F.
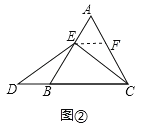
∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠A=60°，AB=AC=BC.
∵EF∥BC，
∴∠AEF=∠ABC=60°，∠AFE=∠ACB=60°，
∴∠AEF=∠AFE=∠A=60°，
∴△AEF是等边三角形，
∴AE=EF=AF，
∴AB﹣AE=AC﹣AF，
∴BE=CF.
∵∠ABC=∠ACB=∠AFE=60°，
∴∠DBE=∠EFC=120°，且AE=EF=DB，BE=CF，
∴△DBE≌△EFC(SAS)，
∴DE=CE，
（3）如图③，将△ABC沿AB翻折得到△ABC'，连接C'F交AB于点E'，连接CE'，DE'，过点F作FH⊥AC'于点H.
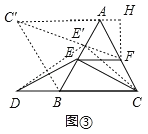
∵将△ABC沿AB翻折得到△ABC'，
∴AC=AC'=BC=BC'=4，∠BAC=∠BAC'=60°，且AE'=AE'，
∴△ACE'≌△AC'E'(SAS)，
∴C'E'=CE'，
由（2）可知：DE'=CE'，
∴C'E'=CE'=DE'.
∵DE+EF=C'E+EF=C'E'+EF，
∴当点C'，点E'，点F三点共线时，DE+EF的值最小.
∵F是AC的中点，
∴AF=CF=2，且HF⊥AC'，∠FAH=180°﹣∠CAB﹣∠C'AB=60°，
∴AH=1，HFAH，
∴C'H=4+1=5，
∴C'F
，
∴DE+EF的最小值为.
