题目内容
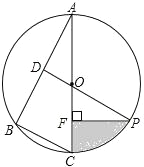
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F ,且DC=FC,点D的坐标为(12,-2).
(1)判断⊙P与x轴的位置关系,并说明理由;
(2)求⊙P半径;
(3)若弧BD上有一动点M,连接AM,过B点作BN⊥AM,垂足为N,连DN,则DN的最小值是 .

【答案】(1)⊙P与x轴相切(2)10(3)![]()
【解析】
(1)答:⊙P与x轴相切.理由如下:
如图,连接CP.
∵AP=PD,DC=CF
∴CP∥AF .
∴∠PCE=∠AOC=90°,即PC⊥x轴.
 又PC是半径,
又PC是半径,
∴⊙P与x轴相切;
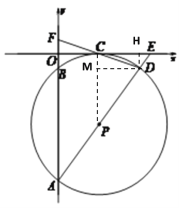
(2)证明:如图,过点D作DH⊥x轴于点H,
则∠CHD=∠COF=90°.
又∵∠FCO=∠DCH,DC=FC
∴△FOC≌△DHC(AAS),
∴OC=HC=6.
过点D作DM⊥PC于点M
设PD = PC = r,
易得DM=HC=6,CM=DH=2
∴PM=r-2
用勾股定理求得r=10.
(3)DN的最小值是![]() ┈
┈
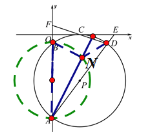
∵∠ONA=90°,∴N是在以AB为直径的圆上,当N是AB中点与D的连线与圆的交点时,DN最小.可求得DN最小值为![]() .
.

练习册系列答案
相关题目