题目内容
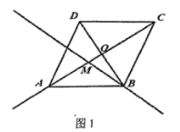
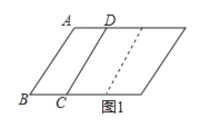
【题目】如图1,已知直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,且AB//CD,若
上,且AB//CD,若![]() 保持不动,线段
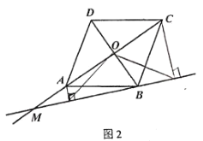
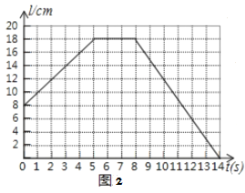
保持不动,线段![]() 先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了
先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了![]() 的长度
的长度![]() 随时间
随时间![]() 的变化而变化的情况,则
的变化而变化的情况,则
(1)在线段![]() 开始平移之前,
开始平移之前,![]() _______
_______![]() ;
;
(2)线段![]() 边向右平移了_______
边向右平移了_______![]() ,向右平移的速度是______
,向右平移的速度是______![]() ;
;
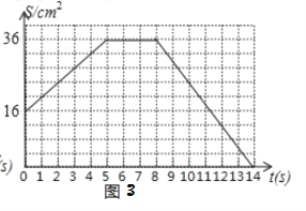
(3)图3反映了变化过程中![]() 的面积
的面积![]() 随时间
随时间![]() 变化的情况.
变化的情况.
①平行线![]() ,
,![]() 之间的距离为_______
之间的距离为_______![]() ;
;
②当![]() 时,面积S的值为_____
时,面积S的值为_____![]() ;
;
③当![]() 时,直接写出
时,直接写出![]() 关于
关于![]() 的函数关系式______(可以不化简).
的函数关系式______(可以不化简).
【答案】(1)8;(2)5,2;(3)①4;②24;③S=-6t+84(8≤t≤14).
【解析】
(1)根据CD从t=0时开始平移,在图2中找出对应的L的值即可得BC的长;
(2)由图2可得线段CD平移5s时BC的长增加了10cm,可得到中间停止时的平移距离,根据速度=距离÷时间即可得平移速度;
(3)①设m、n之间的距离为x,由图2、图3可知BC=8时,△ABC的面积为16,根据三角形的面积公式即可求出x的值,可得答案;
②由题2可知t=2时,BC=12,利用三角形面积公式即可求出S的值;
③由图2可知向左平移的距离为18cm,可求出平移速度,根据平移时间为(t-8)s,利用三角形面积公式即可得答案.
(1)∵CD开始平移时,t=0,
∴由图2可知:t=0时,L=8,
∴在线段![]() 开始平移之前,
开始平移之前,![]() 8cm,
8cm,
故答案为:8
(2)∵t为5到8s时,L的长不变,
∴CD运动到5s时停止,即CD向右平移了5s,
∵t=5时,L=18,
∴CD平移的距离为18-8=10cm,
∴CD向右平移的速度为10÷5=2cm/s,
故答案为:5,2
(3)①设m、n之间的距离为xcm,
由图2和图3可知:CD平移前BC=8,S=16,
∴S=![]() BC·x=16,
BC·x=16,
解得:x=4,即m、n之间的距离为4cm,
故答案为:4
②由图2可知:t=2时,BC=12,
∴S=![]() ×4BC=
×4BC=![]() ×4×12=24cm2,
×4×12=24cm2,
故答案为:24
③由图2、图3可知,向左平移的距离为18cm,平移的时间为6s,
∴向左平移的速度为18÷6=3cm/s,
∴S=![]() ×[18-3(t-8)]×4=-6t+84(8≤t≤14).
×[18-3(t-8)]×4=-6t+84(8≤t≤14).
故答案为:S=-6t+84(8≤t≤14)