��Ŀ����
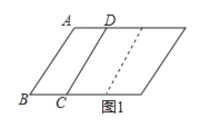
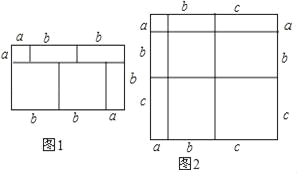
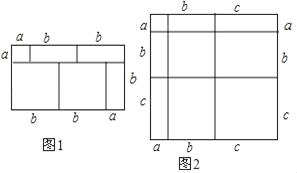
����Ŀ������֪��������һ��ͼ�Σ�ͨ�����ֲ�ͬ�ķ�������������������Եõ�һ�����ֵ�ʽ������ͼ1�����Եõ�(a+2b)(a+b)��a2+3ab+2b2�����������⣺
(1)д��ͼ2������ʾ����ѧ��ʽ_____��
(2)����(1)�����õ��Ľ��ۣ������������⣺��֪a+b+c��9��ab+bc+ac��26����a2+b2+c2��ֵ��
(3)С��ͬѧ��2�ű߳�Ϊa�������Ρ�3�ű߳�Ϊb�������Ρ�5�ű߳�Ϊa��b�ij�����ֽƬƴ����һ�������Σ���ô�ó����νϳ�һ�ߵı߳�Ϊ���٣�
(4)С��ͬѧ����x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ű߳��ֱ�Ϊa��b�ij�����ֽƬƴ����һ�����Ϊ(25a+7b)(2a+5b)�����Σ���9x+10y+6��
���𰸡�(1)(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��(2)29��(3)�ϳ���һ�߳�Ϊ2a+3b��(4)806��
��������
(1)ֱ����������ε����,Ȼ���ٸ��������ε����=�����ε����֮����⼴��;
(2)��a+b+c=9,ab+bc+ac=26����(1)�еõ��Ĺ�ϵʽ,Ȼ����м��㼴��;
(3)���г������ε�����Ĵ���ʽ,Ȼ��ֽ����ʽ,�ɵõ����ε����߳�
(4)�����ε����xa2+yb2+zab=(25a+7b)(9a+5b),Ȼ���������ʽ�˶���ʽ�������(25a+7
b)(2a+45b)�Ľ��,�Ӷ��õ�x��y��z��ֵ,���뼴�����
�⣺(1)�����ε�����ɱ�ʾΪ��(a+b+c)2��
����������a2+b2+c2+2ab+2bc+2ca��
����(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��
�ʴ�Ϊ��(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��
(2)��(1)��֪��a2+b2+c2��(a+b+c)2��2(ab+bc+ca)��92��26��2��81��52��29��
(3)����������2a2+5ab+3b2��(2a+3b)(a+b)��
���Գ����εı߳�Ϊ2a+3b��a+b��
���Խϳ���һ�߳�Ϊ2a+3b��
(4)�߳����ε������xa2+yb2+zab��(25a+7b)(2a+5b)��50a2+14ab+125ab+35b2��50a2+139ab+35b2��
��x��50��y��35��z��139��
��9x+10y+6��450+350+6��806��

 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�