题目内容
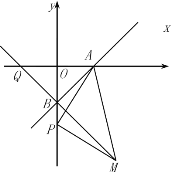
【题目】如图,平面直角坐标系中,点A、B的坐标分别为![]() ,
,![]() ,P为y轴上B点下方一点,
,P为y轴上B点下方一点, ![]() ,以AP为边作等腰直角△APM,其中
,以AP为边作等腰直角△APM,其中![]() ,点M落在第四象限.若直线MB与x轴交于点Q,则Q、M两点中,点_________(填“Q”或“M”)的坐标不随m的变化而变化,该点的坐标为______________.
,点M落在第四象限.若直线MB与x轴交于点Q,则Q、M两点中,点_________(填“Q”或“M”)的坐标不随m的变化而变化,该点的坐标为______________.
【答案】Q; ![]()
【解析】
设直线MB的解析式为y=nx-4,再用m表示点M坐标为(m+4,-m-8).代入MB解析式,求得直线MB的解析式则问题可解.
解:作MN⊥y轴于点N.
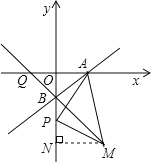
∵△APM为等腰直角三角形,PM=PA,
∴∠APM=90°.
∴∠OPA+∠NPM=90°.
∵∠NMP+∠NPM=90°,
∴∠OPA=∠NMP.
又∵∠AOP=∠PNM=90°,
∴△AOP≌△PNM.(AAS)
∴OP=NM,OA=NP.
∵PB=m(m>0),
∴NM=m+4,ON=OP+NP=m+8.
∵点M在第四象限,
∴点M的坐标为(m+4,-m-8).
设直线MB的解析式为y=nx-4(n≠0).
∵点M(m+4,-m-8).
在直线MB上,
∴-m-8=n(m+4)-4.
整理,得(m+4)n=-m-4.
∵m>0,
∴m+4≠0.
解得n=-1.
∴直线MB的解析式为y=-x-4.
∴无论m的值如何变化,点Q的坐标都为(-4,0).
故答案为:Q;(-4,0)

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目