题目内容
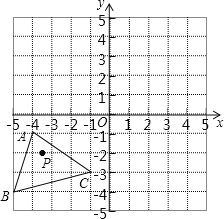
【题目】（1）如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA=3，OB=4，OC=5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．求：
①旋转角的度数；
②线段OD的长；
③∠BDC的度数．
（2）如图2所示，O是等腰直角△ABC（∠ABC=90°）内一点，连接OA、OB、OC，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．当OA、OB、OC满足什么条件时，∠ODC=90°？请给出证明．
【答案】（1）①60°；②4；③150°；（2）OA2+2OB2=OC2时，∠ODC=90°，理由详见解析.
【解析】
（1）①△ABO旋转后AB与BC重合，根据旋转的性质可知∠ABC是旋转角，由△ABC是等边三角形即可知答案.②由旋转的性质可知OB=BD，根据旋转角是60°可知∠OBD=60°即可证明△BOD是等边三角形，进而求出OD的长.③根据OD=4，OC=5，CD=3可证明△OCD是直角三角形，根据△BOD是等边三角形即可求出∠BDC得度数.（2）根据旋转的性质可知旋转角为90°，可证明三角形BOD是等腰直角三角形，进而求出OD=
OB，根据△OCD是直角三角形即可知答案.
（1）①∵△ABC为等边三角形，
∴BA=BC，∠ABC=60°，
∵△BAO绕点B顺时针旋转后得到△BCD，
∴∠OBD=∠ABC=60°，
∴旋转角的度数为60°；
②∵△BAO绕点B顺时针旋转后得到△BCD，
∴BO=BD，
而∠OBD=60°，
∴△OBD为等边三角形；
∴OD=OB=4；
③∵△BOD为等边三角形，
∴∠BDO=60°，
∵△BAO绕点B顺时针旋转后得到△BCD，
∴CD=AO=3，
在△OCD中，CD=3，OD=4，OC=5，
∵32+42=52，
∴CD2+OD2=OC2，
∴△OCD为直角三角形，∠ODC=90°，
∴∠BDC=∠BDO+∠ODC=60°+90°=150°；
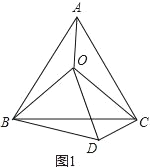
（2）OA2+2OB2=OC2时，∠ODC=90°．理由如下：
∵△BAO绕点B顺时针旋转后得到△BCD，
∴∠OBD=∠ABC=90°，BO=BD，CD=AO，
∴△OBD为等腰直角三角形，
∴OD=OB，
∵当CD2+OD2=OC2时，△OCD为直角三角形，∠ODC=90°，
∴OA2+2OB2=OC2，
∴当OA、OB、OC满足OA2+2OB2=OC2时，∠ODC=90°．
