题目内容
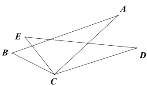
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC.

(1)如果∠B+∠C=120°,则∠AED的度数=______.(直接写出结果)
(2)根据⑴的结论,猜想∠B+∠C与∠AED之间的关系,并说明理由.
【答案】(1)60°;(2)∠AED=![]() (∠B+∠C).理由见解析.
(∠B+∠C).理由见解析.
【解析】
(1)根据四边形的内角和等于360°求出∠BAD+∠CDA,再根据角平分线的定义求出∠EAD+∠EDA,然后根据三角形的内角和等于180°列式计算即可得解;
(2)根据四边形的内角和等于360°表示出∠BAD+∠CDA,再根据角平分线的定义求出∠EAD+∠EDA,然后根据三角形的内角和等于180°列式整理即可得解.
(1)在四边形ABCD中,∵∠B+∠C=120°,∴∠BAD+∠CDA=360°﹣120°=240°.
∵AE平分∠BAD,DE平分∠ADC,∴∠EAD![]() ∠BAD,∠EDA
∠BAD,∠EDA![]() ∠ADC,∴∠EAD+∠EDA
∠ADC,∴∠EAD+∠EDA![]() ∠BAD
∠BAD![]() ∠ADC
∠ADC![]() (∠BAD+∠CDA)
(∠BAD+∠CDA)![]() 240°=120°.
240°=120°.
在△AED中,∠AED=180°﹣(∠EAD+∠EDA)=180°﹣120°=60°.
故答案为:60°.
(2)∠AED![]() (∠B+∠C).理由如下:
(∠B+∠C).理由如下:
在四边形ABCD中,∵∠BAD+∠CDA+∠B+∠C=360°,∴∠BAD+∠CDA=360°﹣(∠B+∠C).
又∵AE平分∠BAD,DE平分∠ADC,∴∠EAD![]() ∠BAD,∠EDA
∠BAD,∠EDA![]() ∠ADC,∴∠EAD+∠EDA
∠ADC,∴∠EAD+∠EDA![]() ∠BAD
∠BAD![]() ∠ADC
∠ADC![]() [360°﹣(∠B+∠C)].
[360°﹣(∠B+∠C)].
在△AED中,∵∠AED=180°﹣(∠EAD+∠EDA)=180°![]() [360°﹣(∠B+∠C)]
[360°﹣(∠B+∠C)]![]() (∠B+∠C),故∠AED
(∠B+∠C),故∠AED![]() (∠B+∠C).
(∠B+∠C).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目