Question

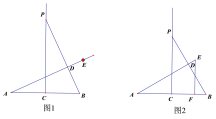
【题目】（1）操作发现：如图1，D是等边三角形ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边三角形DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．

（2）类比猜想：如图2，当动点D运动到等边三角形ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明．

（3）深入探究：①如图3，当动点D在等边三角形ABC的边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF'，连接AF，BF′．探究AF，BF′与AB有何数量关系？并证明你发现的结论。

②如图4，当动点D在等边三角形ABC的边BA的延长线上运动时，其他作法与图3相同，①中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明．

Answer 1

【答案】（1）BD=AF，理由见解析；（2）成立，BD=AF，理由见解析；（3）①AB=AF+BF'，理由见解析；②不成立，新结论为AB=AF-BF'，理由见解析

【解析】

（1）证明△BCD≌△ACF即可解题；

（2）证明△BCD≌△ACF即可解题；

（3）①证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可解题；

②证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可证明新结论．

（1）∵∠BCA=∠DCF，

∴∠BCD=∠ACF，

在△BCD和△ACF中，

BC＝AC，∠BCD＝∠ACF，CF＝CD，

∴△BCD≌△ACF，（SAS），

∴BD=AF；

（2）∵∠BCA=∠DCF，

∴∠BCD=∠ACF，

在△BCD和△ACF中，

BC＝AC，∠BCD＝∠ACF，CF＝CD，

∴△BCD≌△ACF（SAS），

∴BD=AF；

（3）①∵∠BCA=∠DCF，

∴∠BCD=∠ACF，

在△BCD和△ACF中，

BC＝AC，∠BCD＝∠ACF，CF＝CD，

∴△BCD≌△ACF（SAS），

∴BD=AF

∵∠BCA=∠DCF'，

∴∠BCF'=∠ACD，

在△BCF'和△ACD中，

BC＝AC，∠ACD＝∠BCF，′CD＝CF′，

∴△BCF'≌△ACD（SAS），

∴AD=BF'，

∴AB=AF+BF'；

②不成立，新结论为AB=AF-BF'．

证明∵∠BCA=∠DCF，

∴∠BCD=∠ACF，

在△BCD和△ACF中，

BC＝AC，∠BCD＝∠ACF，CF＝CD，

∴△BCD≌△ACF（SAS），

∴BD=AF；

∵∠BCA=∠DCF'，

∴∠BCF'=∠ACD，

在△BCF'和△ACD中，

BC＝AC，∠ACD＝∠BCF′，CD＝CF′，

∴△BCF'≌△ACD（SAS），

∴AD=BF'，

∴AB=AF-BF'．