题目内容
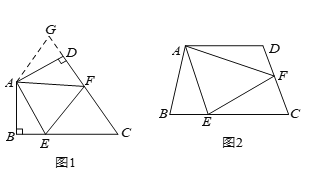
【题目】如图,点 C 为线段 AB 上一点,△ACM、△CBN 都是等边三角形,AN、MC 交于点 E,BM、CN 交于点 F
(1)说明 AN=MB 的理由
(2)△CEF 是什么三角形?为什么?

【答案】(1)见详解;(2)△CEF是等边三角形,理由见详解.
【解析】
(1)等边三角形的性质可以得出△ACN,△MCB两边及其夹角分别对应相等,两个三角形全等,得出线段AN与线段BM相等.
(2)平角的定义得出∠MCN=60°,通过证明△ACE≌△MCF得出CE=CF,根据等边三角形的判定得出△CEF的形状.
(1)证明:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠MCN=180°-∠ACM-∠BCN =60°,∠ACM+∠MCN=∠BCN+∠MCN,
即:∠ACN=∠MCB,
在△ACN和△MCB中
 ,
,
∴△ACN≌△MCB(SAS).
∴AN=BM.
(2)解:△CEF 是等边三角形,理由如下:
∵∠ACM═60°,∠MCN=60°,
∴∠ACM=∠MCN,
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
在△ACE和△MCF中
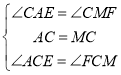
∴△ACE≌△MCF(ASA).
∴CE=CF.
又∵∠MCN=60°,
∴△CEF的形状是等边三角形.

 阅读快车系列答案
阅读快车系列答案【题目】某学校为了解本校七年级学生期末考试数学成绩情况,决定进行抽样分析已知该校七年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有__________.(只要填写序号).
①随机抽取一个班级的学生;
②在全年级学生中随机抽取40名男学生;
③在全年级10个班中各随机抽取4名学生.
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成绩分布统计图(不完整),如图:
①请补充完整频数表;
成绩(分) | 频数 | 频率 |
| __________ | 0.3 |
| __________ | 0.4 |
| 8 | __________ |
| 4 | __________ |
②写出图中![]() 、
、![]() 类圆心角度数;并估计全年级
类圆心角度数;并估计全年级![]() 、
、![]() 类学生大约人数.
类学生大约人数.