ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£ŗ
ĒéŠĪÕ¹Ź¾£ŗ
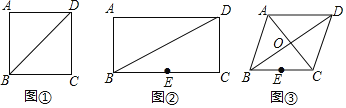
ĒéŠĪŅ»£ŗČēĶ¼![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬ŃŲµČŃüČż½ĒŠĪABCµÄ¶„½Ē
ÖŠ£¬ŃŲµČŃüČż½ĒŠĪABCµÄ¶„½Ē![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬ČōµćBÓėµćCÖŲŗĻ£¬Ōņ³Ę
ÕŪµž£¬ČōµćBÓėµćCÖŲŗĻ£¬Ōņ³Ę![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬ČēĶ¼
µÄ”°ŗĆ½Ē”±£¬ČēĶ¼![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬ĻČŃŲ
ÖŠ£¬ĻČŃŲ![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬¼ōµōÖŲø“²æ·Ö£¬ŌŁ½«ÓąĻĀ²æ·ÖŃŲ
ÕŪµž£¬¼ōµōÖŲø“²æ·Ö£¬ŌŁ½«ÓąĻĀ²æ·ÖŃŲ![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬Čōµć
ÕŪµž£¬Čōµć![]() ÓėµćCÖŲŗĻ£¬Ōņ³Ę
ÓėµćCÖŲŗĻ£¬Ōņ³Ę![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£®
µÄ”°ŗĆ½Ē”±£®
ĒéŠĪ¶ž£ŗČēĶ¼![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬ĻČŃŲ
ÖŠ£¬ĻČŃŲ![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬¼ōµōÖŲø“²æ·Ö£¬ŌŁ½«ÓąĻĀ²æ·ÖŃŲ
ÕŪµž£¬¼ōµōÖŲø“²æ·Ö£¬ŌŁ½«ÓąĻĀ²æ·ÖŃŲ![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬¼ōµōÖŲø“²æ·Ö
ÕŪµž£¬¼ōµōÖŲø“²æ·Ö![]() ÖŲø“ÕŪµžn“Ī£¬×īÖÕČōµć
ÖŲø“ÕŪµžn“Ī£¬×īÖÕČōµć![]() ÓėµćCÖŲŗĻ£¬Ōņ³Ę
ÓėµćCÖŲŗĻ£¬Ōņ³Ę![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬Ģ½¾æ·¢ĻÖ£ŗ
µÄ”°ŗĆ½Ē”±£¬Ģ½¾æ·¢ĻÖ£ŗ![]() ²»·ĮÉč
²»·ĮÉč![]()
![]() ČēĶ¼
ČēĶ¼![]() £¬Čō
£¬Čō![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬Ōņ
µÄ”°ŗĆ½Ē”±£¬Ōņ![]() Óė
Óė![]() µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
![]() ČēĶ¼
ČēĶ¼![]() £¬Čō
£¬Čō![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬Ōņ
µÄ”°ŗĆ½Ē”±£¬Ōņ![]() Óė
Óė![]() µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
![]() ČēĶ¼
ČēĶ¼![]() £¬Čō
£¬Čō![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬Ōņ
µÄ”°ŗĆ½Ē”±£¬Ōņ![]() Óė
Óė![]() µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
µÄŹżĮæ¹ŲĻµŹĒ£ŗ______£®
Ó¦ÓĆĢįÉż£ŗ
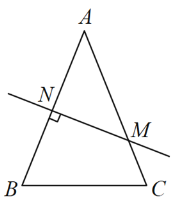
![]() Čē¹ūŅ»øöČż½ĒŠĪµÄČżøö½Ē·Ö±šĪŖ
Čē¹ūŅ»øöČż½ĒŠĪµÄČżøö½Ē·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬![]() £¬ĪŅĆĒ·¢ĻÖ
£¬ĪŅĆĒ·¢ĻÖ![]() ŗĶ
ŗĶ![]() µÄĮ½øö½Ē¶¼ŹĒ“ĖČż½ĒŠĪµÄ”°ŗĆ½Ē”±£»Čē¹ūÓŠŅ»øöČż½ĒŠĪ£¬ĖüµÄČżøö½Ē¾łŹĒ“ĖČż½ĒŠĪµÄ”°ŗĆ½Ē”±£¬ĒŅŅŃÖŖ×īŠ”µÄ½ĒŹĒ
µÄĮ½øö½Ē¶¼ŹĒ“ĖČż½ĒŠĪµÄ”°ŗĆ½Ē”±£»Čē¹ūÓŠŅ»øöČż½ĒŠĪ£¬ĖüµÄČżøö½Ē¾łŹĒ“ĖČż½ĒŠĪµÄ”°ŗĆ½Ē”±£¬ĒŅŅŃÖŖ×īŠ”µÄ½ĒŹĒ![]() £¬ĒóĮķĶāĮ½øö½ĒµÄ¶ČŹż£®
£¬ĒóĮķĶāĮ½øö½ĒµÄ¶ČŹż£®



”¾“š°ø”æ£Ø1£©![]() £» £Ø2£©
£» £Ø2£©![]() £» £Ø3£©
£» £Ø3£©![]() £»
£»
£Ø4£©øĆČż½ĒŠĪµÄĮķĶāĮ½øö½ĒµÄ¶ČŹż·Ö±šĪŖ£ŗ![]() £¬
£¬![]() »ņ
»ņ![]() £¬
£¬![]() .
.
”¾½āĪö”æ
£Ø1£©ÓÉøł¾ŻĢāŅāæÉÖŖ£¬![]() Óė
Óė![]() ÖŲŗĻ£¬¼“
ÖŲŗĻ£¬¼“![]() £»
£»
£Ø2£©øł¾ŻĢāŅāµĆ![]() £¬
£¬![]() £¬ŅņĪŖ
£¬ŅņĪŖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £»
£»
£Ø3£©øł¾ŻÉĻĆę½įĀŪæÉÖŖ£ŗµ±![]() ŹĒ”°ŗĆ½Ē”±£¬ÕŪµžµÄ“ĪŹż¾ĶŹĒ”ĻBĪŖ”ĻCµÄ±¶Źż£¬¼“
ŹĒ”°ŗĆ½Ē”±£¬ÕŪµžµÄ“ĪŹż¾ĶŹĒ”ĻBĪŖ”ĻCµÄ±¶Źż£¬¼“![]() £»
£»
£Ø4£©ÓÉĢāŅāæÉÖŖ£¬Čż½ĒŠĪµÄĮķĶāĮ½øö½Ē¶¼ŹĒ12”汶Źż£¬ŌņæÉÉčĮķĮ½½Ē·Ö±šĪŖ![]() £¬
£¬![]() £¬øł¾ŻČż½ĒŠĪµÄÄŚ½ĒŗĶ¶ØĄķ·ÖĒéæöĒó³öm£¬nµÄÖµ¼“æÉ.
£¬øł¾ŻČż½ĒŠĪµÄÄŚ½ĒŗĶ¶ØĄķ·ÖĒéæöĒó³öm£¬nµÄÖµ¼“æÉ.
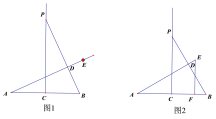
![]() ČēĶ¼1ÖŠ£¬
ČēĶ¼1ÖŠ£¬![]() ŹĒ
ŹĒ![]() µÄ”°ŗĆ½Ē”±£¬
µÄ”°ŗĆ½Ē”±£¬
![]() Óė
Óė![]() ÖŲŗĻ£¬
ÖŲŗĻ£¬
![]() £¬
£¬
¹Ź“š°øĪŖ![]() £»
£»
![]() ČēĶ¼2ÖŠ£¬
ČēĶ¼2ÖŠ£¬![]() ŃŲ
ŃŲ![]() µÄĘ½·ÖĻß
µÄĘ½·ÖĻß![]() ÕŪµž£¬
ÕŪµž£¬
![]() £¬
£¬
ÓÖ![]() ½«ÓąĻĀ²æ·ÖŃŲ
½«ÓąĻĀ²æ·ÖŃŲ![]() µÄĘ½·ÖĻßA1B2ÕŪµž£¬“ĖŹ±µć
µÄĘ½·ÖĻßA1B2ÕŪµž£¬“ĖŹ±µć![]() ÓėµćCÖŲŗĻ£¬
ÓėµćCÖŲŗĻ£¬
![]() £»
£»
![]() Ķā½Ē¶ØĄķ
Ķā½Ē¶ØĄķ![]() £¬
£¬
![]() £»
£»
¹Ź“š°øĪŖ£ŗ![]() £»
£»
![]() øł¾ŻÉĻĆę½įĀŪæÉÖŖ£ŗ
øł¾ŻÉĻĆę½įĀŪæÉÖŖ£ŗ
µ±1“ĪÕŪµžŹ±£¬![]() ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ
ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ![]() £¬
£¬
µ±2“ĪÕŪµžŹ±£¬![]() ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ
ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ![]() £¬
£¬
µ±3“ĪÕŪµžŹ±£¬![]() ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ
ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ![]() £¬
£¬
![]()
µ±n“ĪÕŪµžŹ±£¬![]() ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ
ŹĒ”°ŗĆ½Ē”±£¬ŌņÓŠ![]() £¬
£¬
¹Ź“š°øĪŖ![]() £®
£®
![]() ŅņĪŖ×īŠ”½ĒŹĒ
ŅņĪŖ×īŠ”½ĒŹĒ![]() ŹĒ
ŹĒ![]() µÄŗĆ½Ē£¬
µÄŗĆ½Ē£¬
øł¾ŻŗĆ½Ē¶ØŅ壬ŌņæÉÉčĮķĮ½½Ē·Ö±šĪŖ![]() £¬
£¬![]() ĘäÖŠm”¢n¶¼ŹĒÕżÕūŹż
ĘäÖŠm”¢n¶¼ŹĒÕżÕūŹż![]() £¬
£¬
ÓÉĢāŅā£¬µĆ![]() £¬
£¬
”ą![]() £¬
£¬
”ßm”¢n¶¼ŹĒÕżÕūŹż£¬ĖłŅŌmÓė![]() ŹĒ14µÄÕūŹżŅņ×Ó£¬
ŹĒ14µÄÕūŹżŅņ×Ó£¬
”ą![]() £¬
£¬![]() £¬»ņ
£¬»ņ![]() £¬
£¬![]() £¬
£¬
¼“![]() £¬
£¬![]() £¬»ņ
£¬»ņ![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬![]() £¬»ņ
£¬»ņ![]() £¬
£¬![]() £¬
£¬
ŌņøĆČż½ĒŠĪµÄĮķĶāĮ½øö½ĒµÄ¶ČŹż·Ö±šĪŖ£ŗ![]() £¬
£¬![]() »ņ
»ņ![]() £¬
£¬![]() .
.