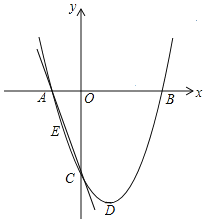
题目内容
【题目】已知抛物线y=x2.
(1)在抛物线上有一点A(1,1),过点A的直线l与抛物线只有一个公共点,直接写出直线l的解析式;
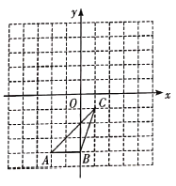
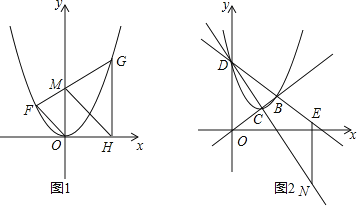
(2)如图1,抛物线有两点F、G,连接FG交y轴于M,过G作x轴的垂线,垂足为H,连接HM、OF,求证:OF∥MH;
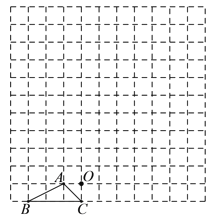
(3)将抛物线y=x2沿直线y=![]() x移动,新抛物线的顶点C,与直线的另一个交点为B,与y轴的交点为D,作直线x=4与直线CD、BD交于点N、E,如图2,求EN的长.
x移动,新抛物线的顶点C,与直线的另一个交点为B,与y轴的交点为D,作直线x=4与直线CD、BD交于点N、E,如图2,求EN的长.
【答案】(1)y=2x﹣1;(2)证明见解析;(3)EN=3.
【解析】
(1)设直线方程为y=kx+b,将点A代入找到k,b的关系,联立抛物线与直线l的表达式并整理得:x2﹣kx+k﹣1=0,△=k2﹣4k+4=0,即可求解;
(2)设F(a,a2),G(b,b2),所以直线FG的解析式为y=(a+b)x﹣ab,M(0,﹣ab),H(b,0),所以直线MH的解析式为=ax﹣ab,直线OF的解析式为y=ax,
所以OF∥MH;
(3)设新抛物线的解析式为y=(x﹣4m)2+3m,联立y=(x﹣4m)2+3m,y=![]() x,得
x,得![]() =4m,
=4m,![]() =4m+
=4m+![]() ,D(0,16m2+3m),所以直线BD的解析式为y=(
,D(0,16m2+3m),所以直线BD的解析式为y=(![]() ﹣4m)x+16m2+3m,直线CD的解析式为y=﹣4mx+16m2+3m.当x=4时,
﹣4m)x+16m2+3m,直线CD的解析式为y=﹣4mx+16m2+3m.当x=4时,![]() =﹣13m+16m2+3,
=﹣13m+16m2+3,![]() =﹣13m﹣16m2,即可求解.
=﹣13m﹣16m2,即可求解.
解:(1)设直线l的表达式为:y=kx+b,
将点A(1,1)的坐标代入上式得![]()
解得![]()
∴直线l的表达式为:y=kx+1﹣k,
![]()
整理得:x2﹣kx+k﹣1=0,
![]() =k2﹣4k+4=0,解得:k=2,
=k2﹣4k+4=0,解得:k=2,
故直线l的表达式为:y=2x﹣1;
(2)设F(a,a2),G(b,b2),
设直线FG的解析式为![]()
将点F,G代入解析式中得
 解得
解得![]()
∴直线FG的解析式为y=(a+b)x﹣ab,
∴M(0,﹣ab),H(b,0).
设直线MH的解析式为![]()
将点M,H代入解析式中得
![]() 解得
解得![]()
∴直线MH的解析式为=ax﹣ab,
设直线OF的解析式为![]()
将点F代入解析式中得
![]() 解得
解得![]()
∴直线OF的解析式为y=ax,
所以OF∥MH;
(3)设新抛物线的解析式为y=(x﹣4m)2+3m,与直线![]() 联立得
联立得
![]()
解得![]() =4m,
=4m,![]() =4m+
=4m+![]() ,
,
∴![]() ,
,![]()
∴![]()
当![]() 时,
时,![]()
∴D(0,16m2+3m),
设直线BD的解析式为![]()
将点B,D代入解析式中得
 解得
解得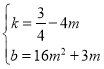
所以直线BD的解析式为y=(![]() ﹣4m)x+16m2+3m,
﹣4m)x+16m2+3m,
设直线CD的解析式为![]()
将点C,D代入解析式中得
![]() 解得
解得![]()
直线CD的解析式为y=﹣4mx+16m2+3m.
当x=4时,![]() =﹣13m+16m2+3,
=﹣13m+16m2+3,![]() =﹣13m﹣16m2,
=﹣13m﹣16m2,
所以EN=3.