题目内容
【题目】在△ABC中,∠ACB=90°,AC=BC,AB=2,现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线AC,直线BC相交于点E,F,我们把DE⊥AC时的位置定为起始位置(如图1),将三角板绕点D顺时针方向旋转一个角度α(0°<α<90°).
(1)如图2,在旋转过程中,当点E在线段AC上时,试判别△DEF的形状,并说明理由;
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形?若存在,求出CG的长,若不存在,说明理由.

【答案】(1)△DEF等腰直角三角形,理由见解析;(2)见解析.
【解析】
(1)连接CD,根据等腰直角三角形的性质得出CD平分∠C,CD⊥AB,进而证得△DCE≌△DFB,从而证得DE=DF,即可判定△DEF是等腰直角三角形.
(2)分三种情况分别讨论,可得出△EFG为等腰三角形时CG的长.
解:(1)△DEF等腰直角三角形.
证明:如图2,∵AC=BC,∠C=90°,D为AB中点,连接CD,
∴CD平分∠C,CD⊥AB,
∵∠DCB=∠B=45°,
∴CD=DB=1,
∵∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
在△DCE和△DFB中,
 ,
,
∴△DCE≌△DFB(ASA),
∴DE=DF,
∴△DEF是等腰直角三角形.
(2)如图3a,当G在线段CB延长线上时,
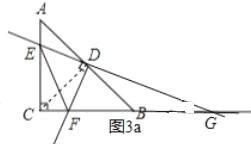
∵∠FGE<45°,∠FEG=45°,∠EFG>90°
∴△EFG不可能是等腰三角形;
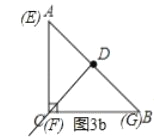
如图3b,当G与C重合时,E与A重合,F与C重合,
此时FE=FG,CG=![]() ,
,
如图3c,当G在线段BC上时,
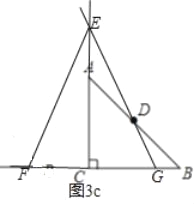
∵∠EGF>45°,∠EFG>45°,∠FEG=45°,
∴只能EF=EG,
∵EC⊥FG,
∴FC=CG,
∵∠EDF=90°,
∴∠FDG=90°,
∴DC=![]() FG=CG,
FG=CG,
∴CG=1;
综上,CG的值为![]() 或1.
或1.