题目内容
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
(1)已知![]() 为智慧三角形,且
为智慧三角形,且![]() 的一边长为,则该智慧三角形的面积为_________;
的一边长为,则该智慧三角形的面积为_________;
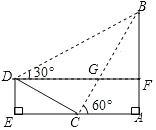
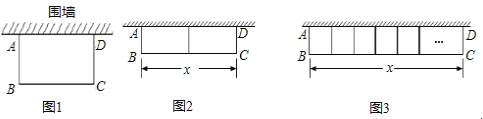
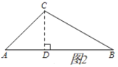
(2)如图①,在![]() 中,
中,![]() ,
,![]() ,求证:
,求证:![]() 是智慧三角形;
是智慧三角形;
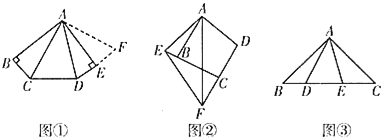
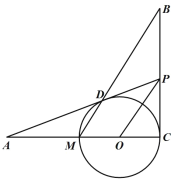
(3)如图②,![]() 是智慧三角形,
是智慧三角形,![]() 为智慧边,
为智慧边,![]() 为智慧角,
为智慧角,![]() ,点
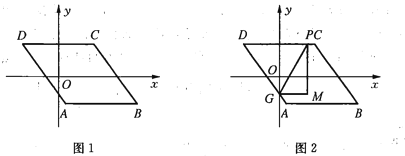
,点![]() 在函数
在函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在点
在点![]() 的上方,且点
的上方,且点![]() 的纵坐标为
的纵坐标为![]() ,当
,当![]() 是直角三角形时,求
是直角三角形时,求![]() 的值.
的值.

【答案】(1)![]() ,
,![]() ,1,
,1,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)由于不确定![]() 是哪条边的边长,故需分3种情况讨论,每种情况中,不确定长
是哪条边的边长,故需分3种情况讨论,每种情况中,不确定长![]() 的边是否为智慧边,故又需要分类讨论;
的边是否为智慧边,故又需要分类讨论;
(2)过C作AB边的垂线CD,构造两个有特殊角的直角三角形,即能用CD把各边关系表示出来,易得BC是AC的![]() 倍,即可得证;
倍,即可得证;
(3)由题意可知![]() ,因此当△ABC为直角三角形时,AB不可能为斜边,即只分
,因此当△ABC为直角三角形时,AB不可能为斜边,即只分![]() 或
或![]() ,两种情况讨论,做辅助线构造三垂直模型,证得相似或全等三角形,再利用对应边的关系把B、C的坐标表示出来,再代入
,两种情况讨论,做辅助线构造三垂直模型,证得相似或全等三角形,再利用对应边的关系把B、C的坐标表示出来,再代入![]() 计算.
计算.
解:(1)如图2,设![]()
①若![]()
1)![]()
![]()
2)![]() ,则
,则![]()
![]()
②若![]()
1)![]() ,即
,即![]()
![]()
2)![]() ,则
,则![]()
![]()
③若![]() ,则
,则![]()
![]()
故答案为:![]() ,
,![]() ,1,
,1,![]()
(2)如图2,过点![]() 作
作![]() 于点
于点![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 是智慧三角形.
是智慧三角形.
(3)由题意可知![]() 或
或![]() .
.
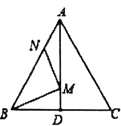
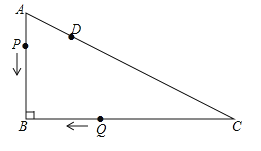
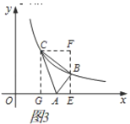
①当![]() 时,如图3,
时,如图3,
过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() 在函数
在函数![]() 的图象上,
的图象上,
∴![]() .
.
解得:![]() ,
,![]() (舍去).
(舍去).
∴![]() .
.
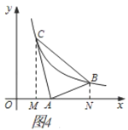
②当![]() 时,如图4,过点
时,如图4,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
则![]() .
.
∴![]() .
.
∴![]() .
.
由(1)知![]() .
.
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() .由①知
.由①知![]() .
.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
∴![]() ,
,![]() .
.
∵点![]() 在函数
在函数![]() (
(![]() )的图象上,
)的图象上,
![]() .
.
解得:![]() .
.
∴![]() .
.
综上所述,![]() 或
或![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目