Question

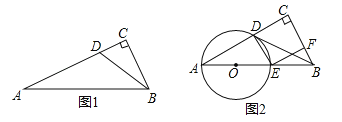
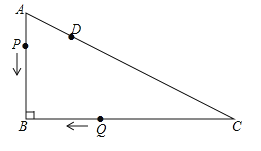
【题目】如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm．点D在AC上，AD=1cm，点P从点A出发，沿AB匀速运动；点Q从点C出发，沿C→B→A→C的路径匀速运动．两点同时出发，在B点处首次相遇后，点P的运动速度每秒提高了2cm，并沿B→C→A的路径匀速运动；点Q保持速度不变，并继续沿原路径匀速运动，两点在D点处再次相遇后停止运动，设点P原来的速度为xcm/s．

（1）点Q的速度为 cm/s（用含x的代数式表示）．

（2）求点P原来的速度．

Answer 1

【答案】（1）x；（2）cm/s．

【解析】试题分析：（1）设点Q的速度为ycm/s，根据题意得方程即可得到结论；

（2）根据勾股定理得到AC的值，求得CD=5﹣1=4，列方程即可得到结论．

试题解析：解：（1）设点Q的速度为ycm/s，由题意得3÷x=4÷y，∴y=x，故答案为： x；

（2）AC===5，CD=5﹣1=4，在B点处首次相遇后，点P的运动速度为（x+2）cm/s，由题意得，解得：x=（cm/s）．

答：点P原来的速度为cm/s．