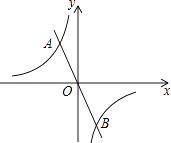题目内容
【题目】如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点，与y轴交于点C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F．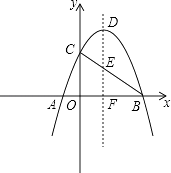
（1）求线段DE的长；
（2）设过E的直线与抛物线相交于点M（x1 ， y1），N（x2 ， y2），试判断当|x1﹣x2|的值最小时，直线MN与x轴的位置关系，并说明理由；
（3）设P为x轴上的一点，∠DAO+∠DPO=∠α，当tan∠α=4时，求点P的坐标．
【答案】
（1）
解：由抛物线y=﹣x2+2x+3可知，C（0，3），
令y=0，则﹣x2+2x+3=0，解得：x=﹣1，x=3，
∴A（﹣1，0），B（3，0）；
∴顶点x=1，y=4，即D（1，4）；
∴DF=4
设直线BC的解析式为y=kx+b，代入B（3，0），C（0，3）得；
，解得 
，
∴解析式为；y=﹣x+3，
当x=1时，y=﹣1+3=2，
∴E（1，2），
∴EF=2，
∴DE=DF﹣EF=4﹣2=2．
（2）
解：设直线MN的解析式为y=kx+b，
∵E（1，2），
∴2=k+b，
∴k=2﹣b，
∴直线MN的解析式y=（2﹣b）x+b，
∵点M、N的坐标是 
的解，
整理得：x2﹣bx+b﹣3=0，
∴x1+x2=b，x1x2=b﹣3；
∵|x1﹣x2|= 
= 
= 
= 
，
∴当b=2时，|x1﹣x2|最小值=2 
，
∵b=2时，y=（2﹣b）x+b=2，
∴直线MN∥x轴．
（3）
解：如图2，∵D（1，4），
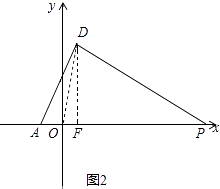
∴tan∠DOF=4，
又∵tan∠α=4，
∴∠DOF=∠α，
∵∠DOF=∠DAO+∠ADO=∠α，
∵∠DAO+∠DPO=∠α，
∴∠DPO=∠ADO，
∴△ADP∽△AOD，
∴AD2=AOAP，
∵AF=2，DF=4，
∴AD2=AF2+DF2=20，
∴OP=19，
同理，当点P在原点左侧，OP=17．
∴P1（19，0），P2（﹣17，0）．
【解析】（1）根据抛物线的解析式即可求得与坐标轴的坐标及顶点坐标，进而求得直线BC的解析式，把对称轴代入直线BC的解析式即可求得．（2）设直线MN的解析式为y=kx+b，依据E（1，2）的坐标即可表示出直线MN的解析式y=（2﹣b）x+b，根据直线MN的解析式和抛物线的解析式即可求得x2﹣bx+b﹣3=0，所以x1+x2=b，x1 x2=b﹣3；根据完全平方公式即可求得∵|x1﹣x2|= = = = ，所以当b=2时，|x1﹣x2|最小值=2 ，因为b=2时，y=（2﹣b）x+b=2，所以直线MN∥x轴．（3）由D（1，4），则tan∠DOF=4，得出∠DOF=∠α，然后根据三角形外角的性质即可求得∠DPO=∠ADO，进而求得△ADP∽△AOD，得出AD2=AOAP，从而求得OP的长，进而求得P点坐标．
【考点精析】本题主要考查了二次函数的图象和两点间的距离的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能正确解答此题．
