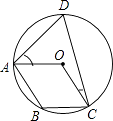题目内容
【题目】已知,如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
试求:(1)![]() 的度数;(2)四边形
的度数;(2)四边形![]() 的面积(结果保留根号);
的面积(结果保留根号);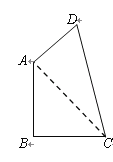
【答案】(1)![]() ;
;
(2)![]()
【解析】
(1)连接AC,由勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACD的形状,进而可求出∠BAD的度数;
(2)由(1)可知△ABC和△ADC是Rt△,再根据S四边形ABCD=S△ABC+S△ADC即可得出结论.
解:(1)连接AC,如图所示:
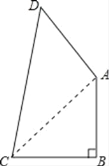
∵AB=BC=1,∠B=90°
∴AC=![]() ,
,
又∵AD=1,DC=![]() ,
,
∴ AD2+AC2=3 CD2=(![]() )2=3
)2=3
即CD2=AD2+AC2
∴∠DAC=90°
∵AB=BC=1
∴∠BAC=∠BCA=45°
∴∠BAD=135°;
(2)由(1)可知△ABC和△ADC是Rt△,
∴S四边形ABCD=S△ABC+S△ADC=1×1×![]() +1×
+1×![]() ×
×![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
x(元/件) | 38 | 36 | 34 | 32 | 30 | 28 | 26 |
t(件) | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
假定试销中每天的销售量t(件)与销售价x(元/件)之间满足一次函数.
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价)