题目内容
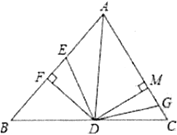
【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
【答案】![]()
【解析】
若△DFE与△DMG全等,则EF=MG,利用已知条件求出EF和MG的长度,建立方程解方程即可求出运动的时间.
设时间为t时,△DFE与△DMG全等,则EF=MG,
①当M在线段CG的延长线上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AFAE=102t,MG=ACCGAM=4t,
即102t=4t,
解得:t=6,
当t=6时,MG=2,所以舍去;
②当M在线段CG上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AFAE=102t,MG=AM(ACCG)=t4,
即102t=t4,
解得:t=![]() ,
,
综上所述当t=![]() 时,△DFE与△DMG全等.
时,△DFE与△DMG全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目