题目内容
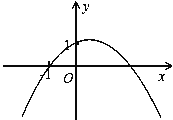
【题目】二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )

A. 0<t<1 B. 0<t<2 C. 1<t<2 D. -1<t<1
【答案】B
【解析】试题分析:此题是压轴题.考查了点与函数的关系,解题的关键是画草图,利用数形结合思想解题.由二次函数的解析式可知,当x=1时,所对应的函数值y=t=a+b+1.把点(﹣1,0)代入y=ax2+bx+1,a﹣b+1=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出t=a+b+1的变化范围.
解:∵二次函数y=ax2+bx+1的顶点在第一象限,
且经过点(﹣1,0),
∴易得:a﹣b+1=0,a<0,b>0,
由a=b﹣1<0得到b<1,结合上面b>0,所以0<b<1①,
由b=a+1>0得到a>﹣1,结合上面a<0,所以﹣1<a<0②,
∴由①+②得:﹣1<a+b<1,
在不等式两边同时加1得0<a+b+1<2,
∵a+b+1=t代入得0<t<2,
∴0<t<2.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目