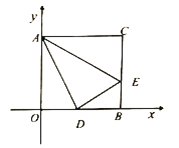
题目内容
【题目】如图1,点![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足
满足![]() ,将点
,将点![]() 、
、![]() 分别向上平移2个单位,再向右平移1个单位至
分别向上平移2个单位,再向右平移1个单位至![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)直接写出点![]() 的坐标:__________;
的坐标:__________;
(2)连接![]() 交
交![]() 于一点
于一点![]() ,求
,求![]() 的值:
的值:
(3)如图2,点![]() 从
从![]() 点出发,以每秒1个单位的速度向上平移运动,同时点
点出发,以每秒1个单位的速度向上平移运动,同时点![]() 从
从![]() 点出发,以每秒2个单位的速度向左平移运动,设射线
点出发,以每秒2个单位的速度向左平移运动,设射线![]() 交
交![]() 轴于
轴于![]() .问
.问![]() 的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
【答案】解:(1)![]() ;(2)
;(2)![]() ;(3)证明略;
;(3)证明略;
【解析】
(1)利用非负数的性质,构建方程组即可解决问题.
(2)利用平行线分线段成比例定理即可解决问题.
(3)结论:S△FMD-S△OFN的值是定值.分两种情形:如图2-1中,当点N在线段OB上时,连接OD.如图2-2中,当点N在BO的延长线上时,连接OD.分别说明即可解决问题.
(1)∵![]() ,
,
又∵(3a+b)2≥0,b-a-4≥0,
∴![]() ,
,
解得![]() ,
,
∴A(-1,0),B(3,0),
∴AB=CD=4,
∵OC=2,CD∥AB,
∴D(4,2),
故答案为(4,2).
(2)如图1中,
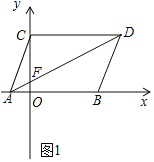
∵CD∥OA,
∴![]() ,
,
∵CD=4,OA=1,
∴![]()
(3)结论:S△FMD-S△OFN的值是定值.
理由:如图2-1中,当点N在线段OB上时,连接OD.
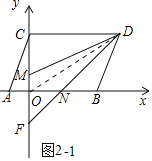
由题意:OM=t,BN=2t,
∴S△OMD=![]() ×t×4=2t,S△DBN=
×t×4=2t,S△DBN=![]() ×2t×2=2t,
×2t×2=2t,
∴S△OMD=S△BND,
∴S四边形DMON=S△OBD=![]() ×3×2=3,
×3×2=3,
∵S△FMD-S△OFN=S四边形DMON=3=定值.
如图2-2中,当点N在BO的延长线上时,连接OD.
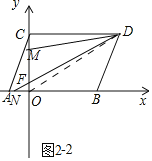
∵S△FMD-S△OFN=S△ODM-S△ODN=S△DBN-S△ODN=S△OBD=3=定值,
综上所述,S△FMD-S△OFN的值是定值,定值为3.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目