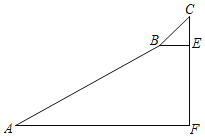
题目内容
【题目】如图在正方形ABCD中,E,F,G,H分别是AD,DC,BC,CD上的点,连接EF,GH.
①若EF⊥GH,则必有EF=GH.
②若EF=GH,则必有EF⊥GH.
判断上述两个命题是否成立,若成立,请说明理由;若不成立,请举出反例.
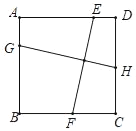
【答案】①②两个命题成立;理由见解析.
【解析】
①作GM⊥CD于M,FN⊥AD于N,证明△EFN≌△HGM(ASA),即可得出EF=GH;
②作GM⊥CD于M,FN⊥AD于N,证明Rt△EFN≌Rt△HGM(HL),得出∠OGQ=∠PFQ,证出∠PQF+∠PFQ=90°,即可得出结论.
上述两个命题成立.理由如下:
①作GM⊥CD于M,FN⊥AD于N,如图所示,则∠GMH=∠FNE=90°.
∵ABCD是正方形,
∴∠A=∠D=90°.
∴ADMG是矩形,
∴GM=AD,
同理可证:NFCD是矩形,
∴NF=DC.
∵四边形ABCD是正方形,
∴AD=DC,
∴FN=GM.
∵∠FND=∠D=∠GMD=90°,
∴∠MON=90°,
∴∠GOF=∠MON=90°,
∴∠OGQ+∠OQG=90°.
∵EF⊥GH,
∴∠PFQ+∠PQF=90°.
∵∠OQG=∠PQF,
∴∠OGQ=∠PFQ.
在△EFN和△HGM中,∵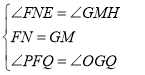 ,
,
∴△EFN≌△HGM(ASA),
∴EF=GH;
②作GM⊥CD于M,FN⊥AD于N,如图所示,则∠GMH=∠FNE=90°.
∵ABCD是正方形,
∴∠A=∠D=90°.
∴ADMG是矩形,
∴GM=AD,
同理可证:NFCD是矩形,
∴NF=DC.
∵四边形ABCD是正方形,
∴AD=DC,
∴FN=GM.
在Rt△EFN和Rt△HGM中,∵![]() ,
,
∴Rt△EFN≌Rt△HGM(HL),
∴∠OGQ=∠PFQ.
∵∠OGQ+∠OQG=90°,∠OQG=∠PQF,
∴∠PQF+∠PFQ=90°,
∴∠FPQ=90°,
∴EF⊥GH.

 名师点拨卷系列答案
名师点拨卷系列答案