Question

【题目】 如图，矩形OABC的边OC在y轴上，边OA在x轴上，C点坐标为（0，3），点D是线段OA上的一个动点，连结CD，以CD为边作矩形CDEF，使边EF过点B．连结OF，当点D与点A重合时，所作矩形CDEF的面积为12．在点D的运动过程中，当线段OF有最大值时，则点F的坐标为______．

Answer 1

【答案】（，+3）

【解析】

连接BD，由矩形的性质得出S矩形CDEF=2S△CBD=12，S矩形OABC=2S△CBD，得出S矩形OABC=12，由OC=3，得出OA=4，由∠CFB=90°，C、B均为定点，F可以看作是在以BC为直径的圆上，取BC的中点M，则OF的最大值=OM+BC=+2，即O、M、F三点共线，设点F的横坐标为2x，则纵坐标为3x，由勾股定理得出方程求解即可得出结果．

解：当点D与点A重合时，如图：

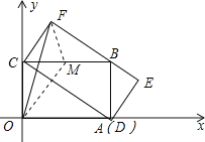
∵S矩形CDEF=2S△CBD=12，S矩形OABC=2S△CBD，

∴S矩形OABC=12，

∵C点坐标为（0，3），

∴OC=3，

∴OA=4，

∵∠CFB=90°，C、B均为定点，

∴F可以看作是在以BC为直径的圆上，取BC的中点M，

则MF=BC=2，OM==，

∴OF的最大值=OM+BC=+2，即O、M、F三点共线，

设点F的横坐标为2x，则纵坐标为3x，

∴（2x）2+（3x）2=（+2）2，

解得：x=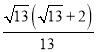（负值舍去）

∴2x=+2，3x=+3

∴点F坐标（，+3）

故答案为：（，+3）