题目内容
推理填空:
完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB="90°(_______________________" )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB="90°(_______________________" )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
垂直定义;同位角相等,两直线平行;两直线平行,同位角相等;∠2=∠BAD;内错角相等,两直线平行
试题分析:先根据垂直的定义证得∠EFB=90°,∠ADB=90°,再根据平行线的判定和性质依次分析即可.
∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(__垂直定义___ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( 同位角相等,两直线平行 )
∴∠1=∠BAD (两直线平行,同位角相等)
又∵∠1=∠2 ( 已知)
∴∠2=∠BAD(等量代换)
∴DG∥BA (内错角相等,两直线平行) .
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
 点出发,要到距离
点出发,要到距离
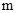 的
的 地去,先沿北偏东
地去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了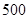

 方向上
方向上 方向上
方向上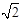
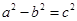

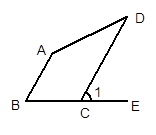
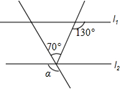
 ,且
,且 ,
, ,则∠AEC= .
,则∠AEC= .