题目内容
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1，0)，B(x2，0)(0＜x1＜x2)两点.
(1)若点A(0.5，0)和点B(1.5，0)，求抛物线的表达式；
(2)三角形的内心是________的交点.在(1)的条件下，抛物线与y轴交于点C，点D在x轴上，且坐标为(-3，0)，直线l经过点C、D．在抛物线上是否存在一点P，使△DCP的内心在y轴上，若存在，求出点P的坐标，若不存在，请说明理由；
(3)是否存在整数a，b，使得1＜x1＜2和1＜x2＜2同时成立？证明你的结论．
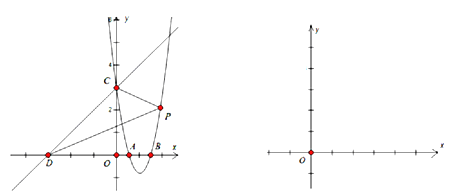
图1 图2
【答案】（1）y=4x2－8x+3；（2）三条角平分线， P(
)；（3）不存在；理由见解析.
【解析】试题分析：（1）把A(0.5，0)和B(1.5，0)代入抛物线解析式，解方程组即可得到结论；
（2）三角形的内心是三条角平分线的交点．设△DCP的内心为M，由OD=OC=3，得到∠DCO=45°，∠PCO=45°，设直线PC交x轴于K，则△COK是等腰直角三角形，得到OK=OC=3，易求直线CP的解析式为y=-x+3．联立二次函数和直线CP组成方程组，解方程组即可得到P的坐标；
(3)假设存在．由题意，建立不等式组
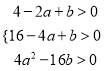且1＜﹣
＜2，得到4＜a＜8，
由于a是整数，故a=5 或6或7，分别代入不等式组，即可得到结论．
试题解析：解：（1）把A(0.5，0)和B(1.5，0)代入得： 
，解得： 
，∴抛物线的解析式为：y=4x2－8x+3；
（2）三角形的内心是三条角平分线的交点．设△DCP的内心为M，∴∠DCO=∠PCO．∵OD=OC=3，∴∠DCO=45°，∴∠PCO=45°，设直线PC交x轴于K，则△COK是等腰直角三角形，∴OK=OC=3，易求直线CP的解析式为y=-x+3．解方程组
，得： 
（舍去），
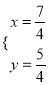，∴P（
， 
）；
(3)不存在．理由：假设存在．由题意可知：
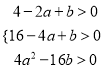且1＜﹣
＜2，∴4＜a＜8，
∵a是整数，∴a=5 或6或7，
当a=5时，代入不等式组，不等式组无解．
当a=6时，代入不等式组，不等式组无解．
当a=7时，代入不等式组，不等式组无解．
综上所述：不存在整数a、b，使得1＜x1＜2和1＜x2＜2同时成立．
