题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
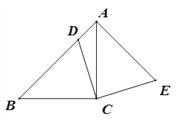
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
【答案】证明:(1)∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴∠DCE=90°,CD=CE,
∵∠ACB=90°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中
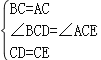 ,
,
∴△BCD≌△ACE,
∴∠B=∠CAE=45°,
∴∠BAE=45°+45°=90°,
∴AB⊥AE;
(2)∵![]() ,
,
而BC=AC,
∴![]() ,
,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,
∴四边形ADCE为矩形,
∵CD=CE,
∴四边形ADCE为正方形
【解析】试题分析:(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
解答:证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE,
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE,
∴∠B=∠CAE=45°,∴∠BAE=45°+45°=90°,∴AB⊥AE;
(2)∵BC2=ADAB,而BC=AC,∴AC2=ADAB,
∵∠DAC=∠CAB,∴△DAC∽△CAB,∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形,
∵CD=CE,∴四边形ADCE为正方形.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1)按表格数据格式,表中的a=;b=;
(2)请估计:当次数s很大时,摸到白球的频率将会接近;
(3)请推算:摸到红球的概率是(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.