题目内容
【题目】某公司装修需用A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | M | N |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m= ,n= ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?

【答案】(1)m=0,n=3;
(2)y=120﹣![]() x,z=60﹣
x,z=60﹣![]() x;
x;
(3)Q=180﹣![]() x;当x=90时,Q最小,时按三种裁法分别裁90张、75张、0张.
x;当x=90时,Q最小,时按三种裁法分别裁90张、75张、0张.
【解析】
试题(1)按裁法二裁剪时,2块A型板材块的长为120cm,150﹣120=30,所以无法裁出B型板,按裁法三裁剪时,3块B型板材块的长为120cm,120<150,而4块块B型板材块的长为160cm>150所以无法裁出4块B型板;
(2)由题意得:共需用A型板材240块、B型板材180块,又因为满足x+2y=240,2x+3z=180,然后整理即可求出解析式;
(3)由题意,得Q=x+y+z=x+120﹣![]() x+60﹣
x+60﹣![]() x和
x和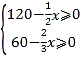 ,[注:事实上,0≤x≤90且x是6的整数倍].由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
,[注:事实上,0≤x≤90且x是6的整数倍].由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
试题解析:(1)按裁法二裁剪时,2块A型板材块的长为120cm,150﹣120=30,所以无法裁出B型板,
按裁法三裁剪时,3块B型板材块的长为120cm,120<150,
而4块块B型板材块的长为160cm>150cm,所以无法裁出4块B型板;
∴m=0,n=3;
(2)由题意得:共需用A型板材240块、B型板材180块,
又∵满足x+2y=240,2x+3z=180,
∴整理即可求出解析式为:y=120﹣![]() x,z=60﹣
x,z=60﹣![]() x;
x;
(3)由题意,得Q=x+y+z=x+120﹣![]() x+60﹣
x+60﹣![]() x.
x.
整理,得Q=180﹣![]() x.
x.
由题意,得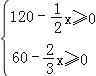
解得x≤90.
[注:事实上,0≤x≤90且x是6的整数倍]
由一次函数的性质可知,当x=90时,Q最小.
由(2)知,y=120﹣![]() x=120﹣
x=120﹣![]() ×90=75,z=60﹣
×90=75,z=60﹣![]() x=60﹣
x=60﹣![]() ×90=0;
×90=0;
故此时按三种裁法分别裁90张、75张、0张.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | ﹣4 | ﹣4 | 0 | 8 |
(1)根据上表填空; ①方程ax2+bx+c=0的两个根分别是和 .
②抛物线经过点(﹣3,);
③在对称轴左侧,y随x增大而;
(2)求抛物线y=ax2+bx+c的解析式.