题目内容
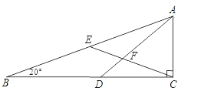
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

【答案】①②④
【解析】
①连接EG.根据等角的余角相等即可得到结果,故①正确;②由BE、AG分别是∠ABC、∠DAC的平分线.得到∠ABF=∠EBD.由于∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,得到∠AFE=∠AEF,根据等腰三角形的性质可得②正确;③如果∠EBC=∠C,则∠C=![]() ∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
①连接EG.
∵∠BAC=90°,AD⊥BC.
∴∠C+∠ABC=90°,∠C+∠DAC=90°,∠ABC+∠BAD=90°.
∴∠ABC=∠DAC,∠BAD=∠C,故①正确;
②∵BE、AG分别是∠ABC、∠DAC的平分线,
∴∠ABF=∠EBD.
∵∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,
∴∠AFE=∠AEF.
∴AF=AE,故②正确;
③如果∠EBC=∠C,则∠C=![]() ∠ABC,
∠ABC,
∵∠BAC=90°,
那么∠C=30°,但∠C≠30°,故③错误;
④∵AG是∠DAC的平分线,
∴AN⊥BE,FN=EN,
在△ABN与△GBN中,∵![]()
∴△ABN≌△GBN.
∴AN=GN.
∴四边形AFGE是平行四边形.
∴GF∥AE.
即GF∥AC.故④正确;
⑤∵AE=AF,AE=FG,
而△AEF不是等边三角形,
∴EF≠AE.
∴EF≠FG,故⑤错误.
故答案为:①②④.

 阅读快车系列答案
阅读快车系列答案【题目】某公司装修需用A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | M | N |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m= ,n= ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?