题目内容
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题. 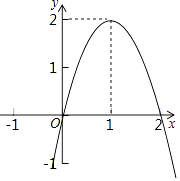
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k无实数根,写出k的取值范围.
【答案】
(1)解:由图象可得:x1=0,x2=2
(2)解:结合图象可得:x<0或x>2时,y<0,
即不等式ax2+bx+c<0的解集为x<0或x>2
(3)解:根据图象可得,k>2时,方程ax2+bx+c=k没有实数根
【解析】(1)找到抛物线与x轴的交点,即可得出方程ax2+bx+c=0的两个根;(2)找出抛物线在x轴下方时,x的取值范围即可;(3)根据图象可以看出k取值范围.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

【题目】某公司装修需用A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | M | N |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m= ,n= ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?