题目内容
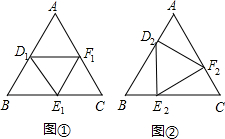
如图,△ABC为正三角形,面积为S.D1,E1,F1分别是△ABC三边上的点,且AD1=BE1=CF1=
AB,可得△D1E1F1,则△D1E1F1的面积S1=______;如,D2,E2,F2分别是△ABC三边上的点,且AD2=BE2=CF2=
AB,则△D2E2F2的面积S2=______;按照这样的思路探索下去,Dn,En,Fn分别是△ABC三边上的点,且
ADn=BEn=CFn=
AB,则Sn=______.
| 1 |
| 2 |
| 1 |
| 3 |
ADn=BEn=CFn=
| 1 |
| n+1 |

∵△ABC为正三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD1=BE1=CF1=
AB,
∴BD1=CE1=AF1=
AB,
∴△AD1F1≌△BD1E1≌△CE1F1,
设等边△ABC的边长为a,
则S=
a2sin60°,
△AD1F1的面积=
×
a•
a•sin60°=
S,
∴△D1E1F1的面积S1=S-3×
S=
S;
同理,AD2=BE2=CF2=
AB时,
BD2=CE2=AF2=
AB,
△AD2F2的面积S2=
×
a•
a•sin60°=
S,
△D2E2F2的面积S2=S-3×
S=
S;
ADn=BEn=CFn=
AB时,
BDn=CEn=AFn=
AB,
△ADnFn的面积=
×
a•
a•sin60°=
S,
△DnEnFn的面积Sn=S-3×
S=
S.
故答案为:
S,
S,
S.
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD1=BE1=CF1=
| 1 |
| 2 |
∴BD1=CE1=AF1=
| 1 |
| 2 |
∴△AD1F1≌△BD1E1≌△CE1F1,
设等边△ABC的边长为a,
则S=
| 1 |
| 2 |
△AD1F1的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴△D1E1F1的面积S1=S-3×
| 1 |
| 4 |
| 1 |
| 4 |
同理,AD2=BE2=CF2=
| 1 |
| 3 |
BD2=CE2=AF2=
| 2 |
| 3 |
△AD2F2的面积S2=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
△D2E2F2的面积S2=S-3×
| 2 |
| 9 |
| 1 |
| 3 |
ADn=BEn=CFn=
| 1 |
| n+1 |
BDn=CEn=AFn=
| n |
| n+1 |
△ADnFn的面积=
| 1 |
| 2 |
| 1 |
| n+1 |
| n |
| n+1 |
| n |
| (n+1)2 |
△DnEnFn的面积Sn=S-3×
| n |
| (n+1)2 |
| n2-n+1 |
| (n+1)2 |
故答案为:
| 1 |
| 4 |
| 1 |
| 3 |
| n2-n+1 |
| (n+1)2 |

练习册系列答案
相关题目