题目内容
已知:等边△ABC的边长为a.
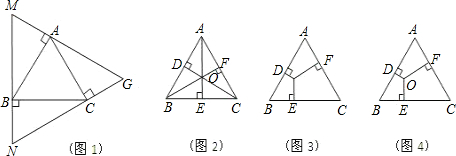
探究(1):如图1,过等边△ABC的顶点A、B、C依次作AB、BC、CA的垂线围成△MNG,求证:△MNG是等边三角形且MN=
a;
探究(2):在等边△ABC内取一点O,过点O分别作OD⊥AB、OE⊥BC、OF⊥CA,垂足分别为点D、E、F.
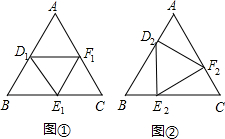
①如图2,若点O是△ABC的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1. OD+OE+OF=
a;结论2. AD+BE+CF=
a;
②如图3,若点O是等边△ABC内任意一点,则上述结论1,2是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
探究(1):如图1,过等边△ABC的顶点A、B、C依次作AB、BC、CA的垂线围成△MNG,求证:△MNG是等边三角形且MN=
| 3 |
探究(2):在等边△ABC内取一点O,过点O分别作OD⊥AB、OE⊥BC、OF⊥CA,垂足分别为点D、E、F.
①如图2,若点O是△ABC的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1. OD+OE+OF=
| ||
| 2 |
| 3 |
| 2 |
②如图3,若点O是等边△ABC内任意一点,则上述结论1,2是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.

(1)证明:如图1,∵△ABC为等边三角形,
∴∠ABC=60°.
∵BC⊥MN,BA⊥MG,
∴∠CBM=∠BAM=90°.
∴∠ABM=90°-∠ABC=30°.
∴∠M=90°-∠ABM=60°.
同理:∠N=∠G=60°.
∴△MNG为等边三角形.
在Rt△ABM中,BM=
=
=
a,
在Rt△BCN中,BN=
=
=
a,
∴MN=BM+BN=
a.
(2)②:结论1成立.
证明:如图3,过点O作GH∥BC,分别交AB、AC于点G、H,过点H作HM⊥BC于点M,
∴∠DGO=∠B=60°,∠OHF=∠C=60°,
∴△AGH是等边三角形,
∴GH=AH.
∵OE⊥BC,
∴OE∥HM,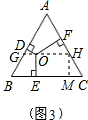
∴四边形OEMH是矩形,
∴HM=OE.
在Rt△ODG中,OD=OG•sin∠DGO=OG•sin60°=
OG,
在Rt△OFH中,OF=OH•sin∠OHF=OH•sin60°=
OH,
在Rt△HMC中,HM=HC•sinC=HC•sin60°=
HC,
∴OD+OE+OF=OD+HM+OF=
OG+
HC+
OH
=
(GH+HC)=
AC=
a.
(2)②:结论2成立.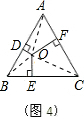
证明:如图4,连接OA、OB、OC,根据勾股定理得:
BE2+OE2=OB2=BD2+OD2①,
CF2+OF2=OC2=CE2+OE2②,
AD2+OD2=AO2=AF2+OF2③,
①+②+③得:BE2+CF2+AD2=BD2+CE2+AF2,
∴BE2+CF2+AD2=(a-AD)2+(a-BE)2+(a-CF)2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
整理得:2a(AD+BE+CF)=3a2
∴AD+BE+CF=
a.
∴∠ABC=60°.
∵BC⊥MN,BA⊥MG,
∴∠CBM=∠BAM=90°.
∴∠ABM=90°-∠ABC=30°.
∴∠M=90°-∠ABM=60°.
同理:∠N=∠G=60°.
∴△MNG为等边三角形.
在Rt△ABM中,BM=
| AB |
| sinM |
| a |
| sin60° |
2
| ||
| 3 |
在Rt△BCN中,BN=
| BC |
| tanN |
| a |
| tan60° |
| ||
| 3 |
∴MN=BM+BN=
| 3 |
(2)②:结论1成立.
证明:如图3,过点O作GH∥BC,分别交AB、AC于点G、H,过点H作HM⊥BC于点M,
∴∠DGO=∠B=60°,∠OHF=∠C=60°,
∴△AGH是等边三角形,
∴GH=AH.
∵OE⊥BC,
∴OE∥HM,

∴四边形OEMH是矩形,
∴HM=OE.
在Rt△ODG中,OD=OG•sin∠DGO=OG•sin60°=
| ||
| 2 |
在Rt△OFH中,OF=OH•sin∠OHF=OH•sin60°=
| ||
| 2 |
在Rt△HMC中,HM=HC•sinC=HC•sin60°=
| ||
| 2 |
∴OD+OE+OF=OD+HM+OF=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)②:结论2成立.

证明:如图4,连接OA、OB、OC,根据勾股定理得:
BE2+OE2=OB2=BD2+OD2①,
CF2+OF2=OC2=CE2+OE2②,
AD2+OD2=AO2=AF2+OF2③,
①+②+③得:BE2+CF2+AD2=BD2+CE2+AF2,
∴BE2+CF2+AD2=(a-AD)2+(a-BE)2+(a-CF)2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
整理得:2a(AD+BE+CF)=3a2
∴AD+BE+CF=
| 3 |
| 2 |

练习册系列答案
相关题目
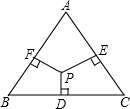
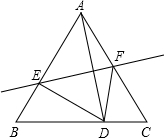 作AD的垂直平分线分别与边AB、AC交于点E、F.
作AD的垂直平分线分别与边AB、AC交于点E、F.