题目内容
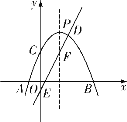
【题目】如图,抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 的对称轴交于点
的对称轴交于点![]() ,与
,与![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 能否与点
能否与点![]() 关于
关于![]() 轴的对称点重合?若认为能,请求出
轴的对称点重合?若认为能,请求出![]() 的值;若认为不能,说明理由;
的值;若认为不能,说明理由;
(3)小林研究了抛物线![]() 的解析式后,得到了如下的结论:因为
的解析式后,得到了如下的结论:因为![]() 可以取任意实数,所以点
可以取任意实数,所以点![]() 可以在
可以在![]() 轴上任意移动,即
轴上任意移动,即![]() 点可以到达
点可以到达![]() 轴的任何位置,你认为他说的有道理吗?说说你的理由;
轴的任何位置,你认为他说的有道理吗?说说你的理由;
(4)当抛物线![]() 与直线
与直线![]() 有两个公共点时,直接写出适合条件的
有两个公共点时,直接写出适合条件的![]() 的最大整数.
的最大整数.
【答案】(1)![]() ;(2)不能,理由见解析;(3)没道理,理由见解析;(4)适合条件的m的最大整数值是1
;(2)不能,理由见解析;(3)没道理,理由见解析;(4)适合条件的m的最大整数值是1
【解析】
解:(1)∵抛物线L:![]() 的对称轴是
的对称轴是![]() ,
,
∴![]() ,
,
∴点F的坐标为![]() ,
,
将点![]() 代入
代入![]() 中,得
中,得![]() ,
,
解得![]() ;
;
(2)不能,
理由:∵点P的坐标为![]() ,点F关于x轴的对称点F′的坐标是
,点F关于x轴的对称点F′的坐标是![]() ,
,
∴若点P与点![]() 重合,则
重合,则![]() ,
,
即![]() ,显然不可能;
,显然不可能;
(3)没道理;
理由:∵点C的纵坐标为![]() ,
,
∴yC的最小值为![]() ,
,
∴无论m取何值,点C都不能到达![]() 以下的位置;
以下的位置;
(4)适合条件的m的最大整数值是1,
【解法提示】∵直线y=kx-1的解析式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,
![]() ,
,
∵抛物线L与直线![]() 有两个公共点,
有两个公共点,
∴当![]() 时,
时,![]() ,
,
∴适合条件的m的最大整数值是1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数![]() (人)与时间
(人)与时间![]() (分钟)的变化情况,数据如下表:(表中9-15表示
(分钟)的变化情况,数据如下表:(表中9-15表示![]() )
)
时间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
人数 | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
【题目】九年级一班邀请![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投票,绘制了如下的打分表和不完整的条形统计图:
五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投票,绘制了如下的打分表和不完整的条形统计图:
五位评委的打分表
A | B | C | D | E | |
甲 | 89 | 91 | 93 | 94 | 86 |
乙 | 88 | 87 | 90 | 98 | 92 |
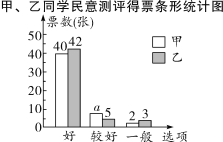
并求得了五位评委对甲同学才艺表演所打分数的平均分和中位数:
![]() (分);中位数是91分.
(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)![]() ________,并补全条形统计图;
________,并补全条形统计图;
(3)为了从甲、乙两人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:
选拔规则:选拔综合分最高的同学参加艺术节演出.其中,综合分=才艺分![]() 测评分
测评分![]() ;
;
才艺分=五位评委所打分数中去掉一个最高分和一个最低分,再算平均分;测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
①当![]() 时,通过计算说明应选拔哪位同学去参加艺术节演出?
时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明![]() 的值不能是多少?
的值不能是多少?