题目内容
【题目】将正方形![]() 的边
的边![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() ,记旋转角为
,记旋转角为![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,
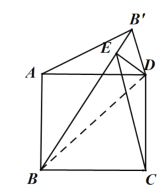
![]() 如图1,当
如图1,当![]() 时,
时,![]() 的形状为 ,连接
的形状为 ,连接![]() ,可求出
,可求出![]() 的值为 ;
的值为 ;

![]() 当
当![]() 且
且![]() 时,
时,
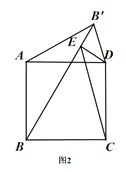
①![]() 中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点![]() 为顶点的四边形是平行四边形时,请直接写出
为顶点的四边形是平行四边形时,请直接写出![]() 的值.
的值.
【答案】(1)等腰直角三角形,![]() ;(2)①结论不变,理由见解析;②3或1.
;(2)①结论不变,理由见解析;②3或1.
【解析】
(1)根据题意,证明![]() 是等边三角形,得
是等边三角形,得![]() ,计算出
,计算出![]() ,根据
,根据![]() ,可得
,可得![]() 为等腰直角三角形;证明
为等腰直角三角形;证明![]() ,可得
,可得![]() 的值;
的值;
(2)①连接BD,通过正方形性质及旋转,表示出![]() ,结合
,结合![]() ,可得
,可得![]() 为等腰直角三角形;证明
为等腰直角三角形;证明![]() ,可得
,可得![]() 的值;
的值;
②分为以CD为边和CD为对角线两种情况进行讨论即可.
(1)由题知![]() °,
°,![]() °,
°,![]()
∴![]() °,且
°,且![]() 为等边三角形
为等边三角形
∴![]() °,
°,![]()
∴![]()
∵![]()
∴![]() °
°
∴![]() °
°
∴![]() 为等腰直角三角形
为等腰直角三角形
连接BD,如图所示

∵![]() °
°
∴![]() 即
即![]()
∵![]()
∴![]()
∴![]()
故答案为:等腰直角三角形,![]()
(2)①两个结论仍然成立
连接BD,如图所示:
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
∵四边形![]() 为正方形
为正方形
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴结论不变,依然成立
②若以点![]() 为顶点的四边形是平行四边形时,分两种情况讨论
为顶点的四边形是平行四边形时,分两种情况讨论
第一种:以CD为边时,则![]() ,此时点
,此时点![]() 在线段BA的延长线上,
在线段BA的延长线上,
如图所示:
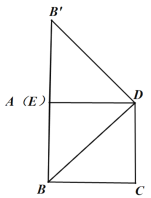
此时点E与点A重合,
∴![]() ,得
,得![]() ;
;
②当以CD为对角线时,如图所示:
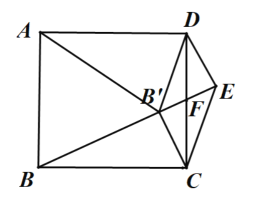
此时点F为CD中点,
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
综上:![]() 的值为3或1.
的值为3或1.

【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种新型商品成本为20元/件,第x天销售量为p件,销售单价为q元,经跟踪调查发现,这40天中p与x的关系保持不变,前20天(包含第20天),q与x的关系满足关系式q=30+ax;从第21天到第40天中,q是基础价与浮动价的和,其中基础价保持不变,浮动价与x成反比.且得到了表中的数据.
X(天) | 10 | 21 | 35 |
q(元/件) | 35 | 45 | 35 |
(1)请直接写出a的值为 ;
(2)从第21天到第40天中,求q与x满足的关系式;
(3)若该网店第x天获得的利润y元,并且已知这40天里前20天中y与x的函数关系式为y=﹣![]() x2+15x+500
x2+15x+500
i请直接写出这40天中p与x的关系式为: ;
ii求这40天里该网店第几天获得的利润最大?