Question

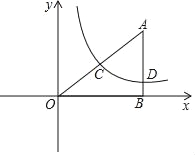
【题目】如图，Rt△ABO在直角坐标系中，AB⊥x轴于点B，AO=10，sin∠AOB=．

（1）若反比例函数y=（x＞0）的图象经过AO的中点C，求k的值；

（2）在（1）的条件下，若反比例函数y=（x＞0）的图象与AB交于点D，当点C，D位于直线l：y=﹣x+b的异侧时，求b的取值范围；

（3）若点D关于y轴的对称点为E，当反比例函数y=的图象和线段AE有公共点时，直接写出k的取值范围．

Answer 1

【答案】（1）12（2）7＜b＜9；（3）﹣12≤k＜0或0＜k≤48

【解析】分析：（1）根据A（8,6），点C是AO的中点，求得C（4,3），进而求得k的值；（2）先求得点C,D的坐标，再根据点C,D位于直线L：y=x+b的异侧，即可求得到b的取值范围；（3）先根据过点E的反比例函数解析式y= ,过点A的反比例函数解析式y= ,再根据反比例函数y= 的图像和线段AE由公共点，即可求得k的取值范围。

详解：（1）∵AO=10，sin∠AOB=，

∴AB=AOsin∠AOB=6，OB=8，即A（8，6），

∵点C是AO的中点，

∴C（4，3），

∵反比例函数y=（x＞0）的图象经过AO的中点C，

∴k=4×3=12；

（2）把x=8代入反比例函数y=，可得y=，

∴D（8，），

把D的坐标代入直线y=﹣x+b，可得b=9，

把C（4，3）代入直线y=﹣x+b，可得b=7，

∵点C，D位于直线l：y=﹣x+b的异侧，

∴7＜b＜9；

（3）∵点D（8，）关于y轴的对称点为E（﹣8，），

∴过点E的反比例函数解析式为y=，

∵A（8，6），

∴过点A的反比例函数解析式为y=，

∵反比例函数y=的图象和线段AE有公共点，

∴﹣12≤k＜0或0＜k≤48．