题目内容
【题目】如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=9,点P在正方形的边上,则满足PE+PF=8的点P的个数是( )
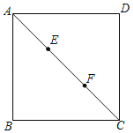
A.8B.6C.4D.0
【答案】A
【解析】
作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H,可得点H到点E和点F的距离之和最小,可求最小值,即可求解.
如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H,
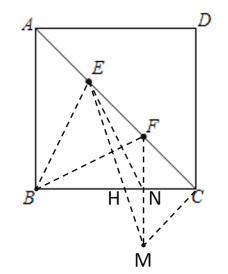
点E,F将对角线AC三等分,且AC=9,
∴EC=6,FC=AE=3,
∵点M与点F关于BC对称,
∴CF=CM=3,![]() ,
,
∴![]() ,
,
∴![]() ,
,
则线段BC存在点H到点E和点F的距离之和最小为![]() ,
,
在点H右侧,当点P与点C重合时,则PE+PF=9,
∴点P在CH上时,![]() ;
;
在点H左侧,当点P与点B重合时,由已知可得![]() ,
,![]() ,
,![]() ,
,
∵AB=AC,CF=AE,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点P在BH上时,![]() ,
,
∴在线段BC上点H的左右两边各有一个点P使得PE+PF=8,同理在线段AB,AD,CD上都存在两个点使得PE+PF=8.
即共有8个点P满足PE+PF=8.
故选:A.

【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种新型商品成本为20元/件,第x天销售量为p件,销售单价为q元,经跟踪调查发现,这40天中p与x的关系保持不变,前20天(包含第20天),q与x的关系满足关系式q=30+ax;从第21天到第40天中,q是基础价与浮动价的和,其中基础价保持不变,浮动价与x成反比.且得到了表中的数据.
X(天) | 10 | 21 | 35 |
q(元/件) | 35 | 45 | 35 |
(1)请直接写出a的值为 ;
(2)从第21天到第40天中,求q与x满足的关系式;
(3)若该网店第x天获得的利润y元,并且已知这40天里前20天中y与x的函数关系式为y=﹣![]() x2+15x+500
x2+15x+500
i请直接写出这40天中p与x的关系式为: ;
ii求这40天里该网店第几天获得的利润最大?